
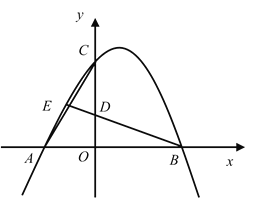
【題目】如圖,已知拋物線![]() 經過點
經過點![]() ,
,![]() ,
,![]() ,點
,點![]() 為
為![]() 中點,連接
中點,連接![]() 、
、![]() ,并延長
,并延長![]() 交
交![]() 于點
于點![]() .
.
(1)求拋物線![]() 的表達式;
的表達式;
(2)若拋物線![]() 與拋物線
與拋物線![]() 關于
關于![]() 軸對稱,在拋物線
軸對稱,在拋物線![]() 位于第二象限的部分上取一點
位于第二象限的部分上取一點![]() ,過點
,過點![]() 作
作![]() 軸,垂足為點
軸,垂足為點![]() ,是否存在這樣的點
,是否存在這樣的點![]() ,使得
,使得![]() 與
與![]() 相似?若存在,請求出點
相似?若存在,請求出點![]() 坐標;若不存在,請說明理由.
坐標;若不存在,請說明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() ,
,![]()
【解析】
(1)設拋物線的解析式為y=ax2+bx+c,將A(1,0),B(2,0),C(0,2)代入拋物線的解析式即可解答;
(2)求出拋物線w2的解析式y=x2x+2,可知點D坐標,證明△AOC∽△DOB,可證出BD⊥AC,則![]() ,設F(m,0),
,設F(m,0),![]() ,m<0,若△QFO與△CDE相似,可分兩種情況考慮,①是△QFO∽△DEC時,②是△QFO∽△CED時,列出相似比即可求出m的值.
,m<0,若△QFO與△CDE相似,可分兩種情況考慮,①是△QFO∽△DEC時,②是△QFO∽△CED時,列出相似比即可求出m的值.
解:(1)設拋物線的解析式為y=ax2+bx+c,將A(1,0),B(2,0),C(0,2)代入拋物線的解析式得: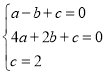 ,
,
解得:a=1,b=1,c=2,
∴拋物線w1的表達式為y=x2+x+2;
(2)∵拋物線w1與拋物線w2關于y軸對稱,
∴拋物線w2的解析式y=x2x+2,
∵點D為OC中點,C(0,2),
∴D(0,1),
∵A(1,0),B(2,0),
∴![]() ,
,
∵∠AOC=∠BOD=90°,
∴△AOC∽△DOB,
∴∠ACO=∠DBO,
∴BD⊥AC,
∴![]() ,
,
設F(m,0),![]() ,m<0,若△QFO與△CDE相似,可分兩種情況考慮:
,m<0,若△QFO與△CDE相似,可分兩種情況考慮:
①△QFO∽△DEC時,
![]()
∴![]() ,
,
解得:![]() (舍去)
(舍去)
∴![]() ,
,
②△QFO∽△CED時,
![]() ,
,
∴![]() ,
,
解得:![]() (舍去)
(舍去)
∴F(-1,0);
綜上所述: ![]() ,
,![]()


科目:初中數學 來源: 題型:
【題目】如圖1,長、寬均為3,高為8的長方體容器,放置在水平桌面上,里面盛有水,水面高為6,繞底面一棱長進行旋轉傾斜后,水面恰好觸到容器口邊緣,圖2是此時的示意圖,則圖2中水面高度為( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形紙片ABCD中,AB=6,BC=10,點E在CD上,將△BCE沿BE折疊,點C恰落在邊AD上的點F處,點G在AF上,將△ABG沿BG折疊,點A恰落在線段BF上的點H處,有下列結論:①∠EBG=45°;②S△ABG=![]() S△FGH;③△DEF∽△ABG;④AG+DF=FG.其中正確的是_____.(把所有正確結論的序號都選上)
S△FGH;③△DEF∽△ABG;④AG+DF=FG.其中正確的是_____.(把所有正確結論的序號都選上)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現有A,B兩種商品,已知買一件A商品比買一件B商品少30元,用160元全部購買A商品的數量與用400元全部購買B商品的數量相同.
(1)A,B兩種商品每件各是多少元?
(2)如果小亮準備購買A,B兩種商品共10件,總費用不超過380元,且不低于300元,那么一共有幾種購買方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
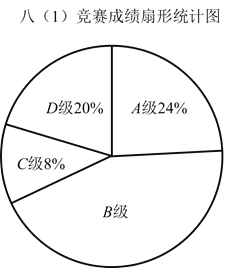
【題目】在學校組織的數學競賽中,八(1)班比賽成績分為![]() 、
、![]() 、
、![]() 、
、![]() 四個等級,其中相應等級的得分依次記為100分,90分,80分,70分,學校將八(1)班成績現整理并繪制成如下的統計圖.請你根據以上提供的信息解答下列問題:
四個等級,其中相應等級的得分依次記為100分,90分,80分,70分,學校將八(1)班成績現整理并繪制成如下的統計圖.請你根據以上提供的信息解答下列問題:
(1)請補全條形統計圖
(2)八年級一班競賽成績眾數是________,中位數落在________類.
(3)若該校有1500名學生,請估計該校本次競賽成績為![]() 類的學生人數.
類的學生人數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,AB=4,E是BC邊的中點, F是CD邊上的一點, 且DF=1.若M、N分別是線段AD、AE上的動點,則MN+MF的最小值為________.
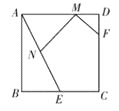
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題提出(1)如圖①,在△ABC中,BC=6,D為BC上一點,AD=4,則△ABC面積的最大值是 .
問題探究(2)如圖②,已知矩形ABCD的周長為12,求矩形ABCD面積的最大值.
問題解決(3)如圖③,△ABC是葛叔叔家的菜地示意圖,其中AB=30米,BC=40米,AC=50米,現在他想利用周邊地的情況,把原來的三角形地拓展成符合條件的面積盡可能大、周長盡可能長的四邊形地,用來建魚塘.已知葛叔叔欲建的魚塘是四邊形ABCD,且滿足∠ADC=60°.你認為葛叔叔的想法能否實現?若能,求出這個四邊形魚塘周長的最大值;若不能,請說明理由.
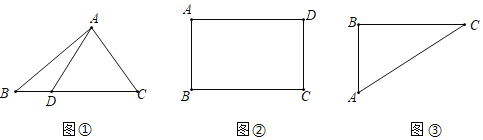
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠ACB=90°,AC=BC,CD平分∠ACB,點D,E關于CB對稱,連接EB并延長,與AD的延長線交于點F,連接DE,CE.對于以下結論:
①DE垂直平分CB;②AD=BE;③∠F不一定是直角;④EF2+DF2=2CD2.
其中正確的是( )
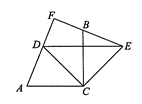
A.①④B.②③C.①③D.②④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com