
如圖①所示,已知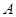 、
、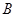 為直線
為直線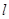 上兩點,點
上兩點,點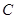 為直線
為直線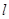 上方一動點,連接
上方一動點,連接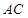 、
、 ,分別以
,分別以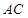 、
、 為邊向
為邊向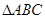 外作正方形
外作正方形 和正方形
和正方形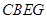 ,過點
,過點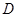 作
作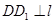 于點
于點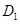 ,過點
,過點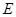 作
作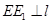 于點
于點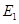 .
.
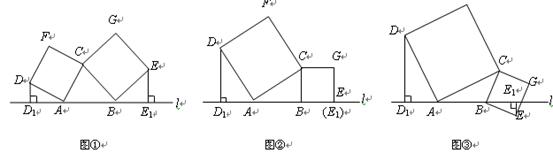
(1)如圖②,當點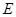 恰好在直線
恰好在直線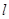 上時(此時
上時(此時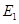 與
與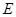 重合),試說明
重合),試說明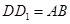 ;
;
(2)在圖①中,當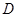 、
、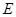 兩點都在直線
兩點都在直線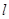 的上方時,試探求三條線段
的上方時,試探求三條線段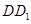 、
、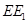 、
、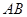 之間的數量關系,并說明理由;
之間的數量關系,并說明理由;
(3)如圖③,當點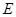 在直線
在直線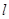 的下方時,請直接寫出三條線段
的下方時,請直接寫出三條線段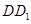 、
、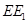 、
、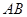 之間的數量關系.(不需要證明)
之間的數量關系.(不需要證明)
解:(1)在正方形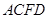 中,∵
中,∵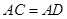 ,
,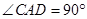 ,
,
∴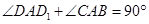 ………………………………………………………………1分
………………………………………………………………1分
又∵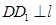 , ∴
, ∴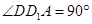 ,∴
,∴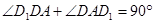 ,
,
∴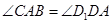 ……………………………………………………………………2分
……………………………………………………………………2分
又∵四邊形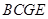 為正方形,∴
為正方形,∴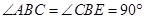 ,∴
,∴ ……3分
……3分
在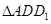 與
與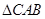 中,
中, ,
,
∴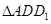 ≌
≌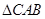 ,∴
,∴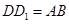 ………………4分
………………4分

(2)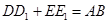 ……………………………5分
……………………………5分
過點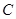 作
作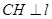 ,垂足為
,垂足為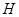 ,
,
由(1)知: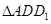 ≌
≌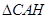 ,
,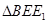 ≌
≌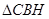 ……………………………………6分
……………………………………6分
∴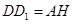 ,
,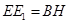 ,∴
,∴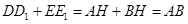 ………………………8分
………………………8分
(3)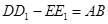 …………………………………………………………………9分
…………………………………………………………………9分
(說明:其它解法,仿此得分)
【解析】(1)由四邊形CADF、CBEG是正方形,可得AD=CA,∠DAC=∠ABC=90°,又由同角的余角相等,求得∠ADD1=∠CAB,然后利用AAS證得△ADD1≌△CAB,根據全等三角形的對應邊相等,即可得DD1=AB;
(2)首先過點C作CH⊥AB于H,由DD1⊥AB,可得∠DD1A=∠CHA=90°,由四邊形CADF是正方形,可得AD=CA,又由同角的余角相等,求得∠ADD1=∠CAH,然后利用AAS證得△ADD1≌△CAH,根據全等三角形的對應邊相等,即可得DD1=AH,同理EE1=BH,則可得AB=DD1+EE1.
(3)證明方法同(2),易得AB=DD1-EE1.


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:初中數學 來源: 題型:
| 1 |
| 6 |
| 2 |
| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源:101網校同步練習 初三數學 華東師大(新課標2001/3年初審) 華東師大版 題型:013
如圖(1)所示,已知BC為等腰三角形紙片ABC的底邊,AD⊥BC,AD=BC,將此紙片沿AD剪開,得到兩個三角形(如圖(2)),若把這兩個三角形拼成一個平面四邊形,則能拼出互不全等的四邊形的個數是

A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
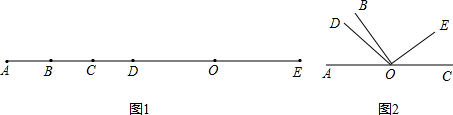
科目:初中數學 來源: 題型:解答題
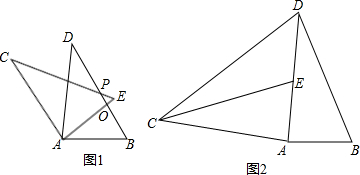
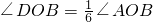 ,
,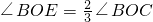 ,∠DOB與∠BOE互余,求∠AOB和∠BOC.
,∠DOB與∠BOE互余,求∠AOB和∠BOC.
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖9所示,已知AB為⊙O的直徑,CD是弦,且AB![]() CD于點E.連接AC、OC、BC.
CD于點E.連接AC、OC、BC.
(1)求證:![]() ACO=
ACO=![]() BCD.
BCD.
(2)若EB=![]() ,CD=
,CD=![]() ,求⊙O的直徑.
,求⊙O的直徑.
![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com