
【題目】正方形![]() 中,
中,![]() 為對角線
為對角線![]() 上一點,且
上一點,且![]() ,
,![]() 交
交![]() 于
于![]() ,延長
,延長![]() 交
交![]() 于
于![]() .
.
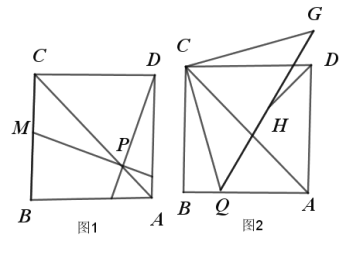
(1)求證:![]() ;
;
(2)已知如圖(2),![]() 為
為![]() 上一點,連接
上一點,連接![]() ,并將
,并將![]() 逆時針旋轉
逆時針旋轉![]() 至
至![]() ,連接
,連接![]() ,
,![]() 為
為![]() 的中點,連接
的中點,連接![]() ,試求出
,試求出![]() .
.
【答案】(1)見解析(2)![]()
【解析】
(1)過點P作PF⊥CD于F點,過點P作PE⊥BC于E點,得到四邊形CFPE是正方形,證明△PME≌△PDF,得到ME=DF,再根據正方形的性質即可求解;
(2)過Q點作QM⊥CD,延長DH交QM于E點,過E點作FN⊥BC交BC于F點,交AD于N點,連接DG,根據題意證明四邊形ENDM是正方形,DE是對角線,過H點作HP⊥AD,根據中位線的性質得到AQ=2HP,根據等腰直角三角形的性質得到DH=![]() HP,故可求出
HP,故可求出![]() 的值.
的值.
(1)過點P作PF⊥CD于F點,過點P作PE⊥BC于E點,
∵∠ECF=90°
∴四邊形CFPE是矩形
∵![]() 為對角線
為對角線![]() 上一點,
上一點,
∴CP平分∠ECF
∴EP=FP
∴矩形CFPE是正方形
∴![]()
∵![]()
∴∠MPF+∠FPD=90°
∵∠MPF+∠MPE=90°
∴∠EPM=∠FPD
又∵EP=FP,∠PEM=∠PFD=90°
∴△PME≌△PDF
∴ME=DF
∴![]() =
=![]() =CE+CF
=CE+CF
∵PC=![]()
∴CE= ![]()
∴![]() ;
;
(2)過Q點作QM⊥CD,延長DH交QM于E點,過E點作FN⊥BC交BC于F點,交AD于N點,
∴四邊形EFBQ是矩形,四邊形ENDM是矩形,
連接DG,
∵![]() 逆時針旋轉
逆時針旋轉![]() 至
至![]() ,
,
∴CQ=CG,CQ⊥CG
∴∠QCD+∠DCG=90°
∵∠QCD+∠BCQ=90°
∴∠BCQ=∠DCG
又∵BC=DC,CQ=CG
∴△BCQ≌△DCG,∠CDG =∠CBQ=90°
∴A,D,G在同一直線上,
∴DG=BQ,
∵MQ⊥CD,AG⊥CD
∴QM∥AG
∴∠EQH=∠DGH,
∵H是GQ的中點,
∴HQ=HG
又∵∠EHQ=∠DHG,
∴△EHQ≌△DHG,
∴EQ=DG
∴BQ=EQ
∴矩形EFBQ是正方形
∴EF=EQ
∴MQ-EQ=FN-EF
∴EM=EN
∴矩形ENDM是正方形,
∴DE是正方形ENDM的對角線,
過H點作HP⊥AG,
∵H點是HG的中點,∠QAG=90°
∴P點是AG中點,
∴AQ=2HP
∵△HDP是等腰直角三角形,HP=DP
∴DH=![]()
∴![]() =
=![]() .
.


科目:初中數學 來源: 題型:
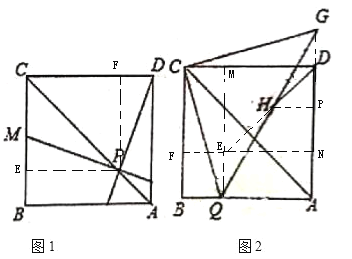
【題目】如圖,一架![]() 的云梯
的云梯![]() 斜靠在一豎直的墻
斜靠在一豎直的墻![]() 上,這時
上,這時![]() 為
為![]() .
.
(1)求這個梯子的底端距墻的垂直距離有多遠;
(2)當![]() ,且
,且![]() 時,AC的長是多少米;
時,AC的長是多少米;
(3)如果梯子![]() 的底端向墻一側移動了2米,那么梯子的頂端向上滑動的距離是多少米?
的底端向墻一側移動了2米,那么梯子的頂端向上滑動的距離是多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
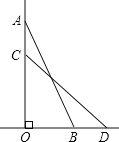
【題目】對于一個圖形,通過兩種不同的方法計算它的面積,可以得到一個數學等式,例如圖1可以得到![]() ,請解答下列問題:
,請解答下列問題:
(1)寫出圖2中所表示的數學等式____________________________________
(2)根據整式乘法的運算法則,通過計算驗證上述等式.
(3)利用(1)中得到的結論,解決下面的問題:
若![]() ,
,![]() ,則
,則![]() _________.
_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的四個頂點分別在四條平行線 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 上,這四條直線中相鄰兩條之間的距離依次為
上,這四條直線中相鄰兩條之間的距離依次為 ![]() 、
、 ![]() 、
、 ![]() (
( ![]() >0,
>0, ![]() >0,
>0, ![]() >0).
>0).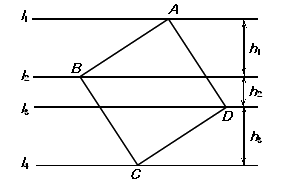
(1)求證: ![]() =
= ![]() ;
;
(2)設正方形ABCD的面積為S,求證:S= ![]() ;
;
(3)若 ![]() ,當
,當 ![]() 變化時,說明正方形ABCD的面積S隨
變化時,說明正方形ABCD的面積S隨 ![]() 的變化情況.
的變化情況.
查看答案和解析>>
科目:初中數學 來源: 題型:
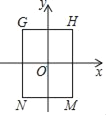
【題目】對于點P(a,b),點Q(c,d),如果a﹣b=c﹣d,那么點P與點Q就叫作等差點.例如:點P(4,2),點Q(﹣1,﹣3),因4﹣2=1﹣(﹣3)=2,則點P與點Q就是等差點.如圖在矩形GHMN中,點H(2,3),點N(﹣2,﹣3),MN⊥y軸,HM⊥x軸,點P是直線y=x+b上的任意一點(點P不在矩形的邊上),若矩形GHMN的邊上存在兩個點與點P是等差點,則b的取值范圍為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是某同學對多項式(x2-4x+2)(x2-4x+6)+4進行因式分解的過程.
解:設x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列問題:
(1)該同學第二步到第三步運用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.兩數和的完全平方公式 |
D.兩數差的完全平方公式 |
(2)該同學因式分解的結果是否徹底?________.(填“徹底”或“不徹底”)若不徹底,請直接寫出因式分解的最后結果_________ .
(3)請你模仿以上方法嘗試對多項式(x2-2x)(x2-2x+2)+1進行因式分解.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的盒子里裝有只有顏色不同的黑、白兩種球共![]() 個,小李做摸球實驗,她將盒子里面的球攪勻后從中隨機摸出一個球記下顏色,再把它放回盒子中,不斷重復上述過程,如表是實驗中的一組統計數據:
個,小李做摸球實驗,她將盒子里面的球攪勻后從中隨機摸出一個球記下顏色,再把它放回盒子中,不斷重復上述過程,如表是實驗中的一組統計數據:
摸球的次數 |
|
|
|
|
|
|
|
摸到白球的次數 |
|
|
|
|
|
|
|
摸到白球的頻率 |
|
|
|
|
|
|
|
![]() 請估計:當實驗次數為
請估計:當實驗次數為![]() 次時,摸到白球的頻率將會接近________;(精確到
次時,摸到白球的頻率將會接近________;(精確到![]() )
)
![]() 假如你摸一次,你摸到白球的概率
假如你摸一次,你摸到白球的概率![]() (摸到白球)
(摸到白球)![]() ________;
________;
![]() 如何通過增加或減少這個不透明盒子內球的具體數量,使得在這個盒子里每次摸到白球的概率為
如何通過增加或減少這個不透明盒子內球的具體數量,使得在這個盒子里每次摸到白球的概率為![]() ?
?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD的對角線相交于點0,AC=2,BD=![]() .將菱形按如圖方式折疊,使點B與點O重合,折痕為EF,則五邊形AEFCD的面積是( )
.將菱形按如圖方式折疊,使點B與點O重合,折痕為EF,則五邊形AEFCD的面積是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】河大附中初一年級有350名同學去春游,已知2輛A型車和1輛B型車可以載學生100人;1輛A型車和2輛B型車可以載學生110人.
(1)A、B型車每輛可分別載學生多少人?
(2)若租一輛A需要100元,一輛B需120元,請你設計租車方案,使得恰好運送完學生并且租車費用最少.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com