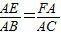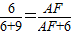Question

已知：AD平分△ABC的∠BAC交BC于D，DE∥AC交AB于E，EF∥BC交AC于F，BE=9，CF=6，則AF的長為（ ）
A．15
B．9
C．6
D．4

Answer 1

【答案】分析：根據DE∥AC交AB于E，EF∥BC交AC于F可得到四邊形EDCF為平行四邊形，從而得到ED=FC，再根據AD平分△ABC的∠BAC交BC于D，得到AE=ED，利用平行線分線段成比例定理即可求得AF的長．
解答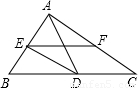：解：∵AD平分△ABC的∠BAC交BC于D，
∴∠BAD=∠CAD，
∵DE∥AC交AB于E，
∴∠CAD=∠ADE，
∴∠EAD=∠EDA，
∴AE=DE，
∵DE∥AC交AB于E，EF∥BC交AC于F
∴四邊形EDCF為平行四邊形，
∴AE=ED=FC=9，
∵DE∥AC交AB于E，BE=9，CF=6，
∴
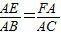
即：
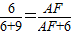
解得AF=4，
故選D．
點評：本題考查了平行四邊形的判定及性質和平行線分線段成比例定理的知識，解題的關鍵是得到AE=ED=FC．