Question

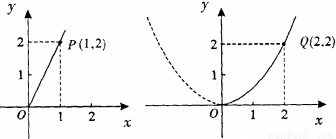
隨著綠城南寧近幾年城市建設的快速發展，對花木的需求量逐年提高．某園林專業戶計劃投資種植花卉及樹木，根據市場調查與預測，種植樹木的利潤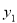與投資量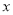成正比例關系，如圖（1）所示；種植花卉的利潤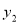與投資量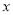成二次函數關系，如圖（2）所示（注：利潤與投資量的單位：萬元）

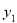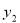（1）分別求出利潤與關于投資量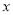的函數關系式；

（2）如果這位專業戶以8萬元資金投入種植花卉和樹木，他至少獲得多少利潤？他能獲取的最大利潤是多少？

Answer 1

（1）y1=2x（x≥0）；y=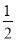x2（x≥0）；（2）當x=8時，z的最大值是32．

【解析】

試題分析：（1）可根據圖象利用待定系數法求解函數解析式；

（2）根據總利潤=樹木利潤+花卉利潤，列出函數關系式，再求函數的最值．

試題解析：（1）設y1=kx，由圖①所示，函數y1=kx的圖象過（1，2），

所以2=k•1，k=2，

故利潤y1關于投資量x的函數關系式是y1=2x（x≥0）；

∵該拋物線的頂點是原點，

∴設y2=ax2，

由圖②所示，函數y2=ax2的圖象過（2，2），

∴2=a•22，a=，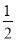

故利潤y2關于投資量x的函數關系式是：y=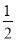x2（x≥0）；

（2）設這位專業戶投入種植花卉x萬元（0≤x≤8），則投入種植樹木（8-x）萬元，他獲得的利潤是z

元，根據題意，

得z=2（8-x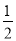）+x2=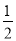x2-2x+16=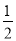（x-2）2+14，

當x=2時，z的最小值是14，

∵0≤x≤8，

∴-2≤x-2≤6，

∴（x-2）2≤36，

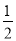∴（x-2）2≤18，

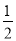∴（x-2）2+14≤18+14=32，

即z≤32，此時x=8，

答：當x=8時，z的最大值是32．

考點：1．二次函數的應用；2．一次函數的應用．