
【題目】如圖,正方形的邊長為2,中心為O,從O、A、B、C、D五點中任取兩點.
(1)求取到的兩點間的距離為2的概率;
(2)求取到的兩點間的距離為![]() 的概率;
的概率;
(3)求取到的兩點間的距離為![]() 的概率.
的概率.

【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】試題分析:AB=BC=CD=AD=2,AC=BD=2![]() ,OD=OC=OA=OB=
,OD=OC=OA=OB=![]() ,求取到的兩點間的距離為2、
,求取到的兩點間的距離為2、![]() 、2
、2![]() 的概率,也就是求取到這些相等線段的概率,總共有10條線段。
的概率,也就是求取到這些相等線段的概率,總共有10條線段。
試題解析:解:(1)從O、A、B、C、D五點中任取兩點,所有等可能出現的結果有:
AB、AC、AD、BC、BD、CD、OA、OB、OC、OD,共有10種,
滿足兩點間的距離為2的結果有AB、BC、CD、AD這4種,
則P(兩點間的距離為2)=![]() .
.
(2)滿足兩點間的距離為![]() 的結果有AC、BD這2種.
的結果有AC、BD這2種.
則P(兩點間的距離為![]() )=
)=![]() .
.
(3)滿足兩點間的距離為![]() 的結果有OA、OB、OC、OD這4種.
的結果有OA、OB、OC、OD這4種.
則P(兩點間的距離為![]() )=
)=![]() .
.


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:初中數學 來源: 題型:
【題目】某電廠有5000噸電煤.
(1)求:這些電煤能夠使用的天數x(單位:天)與該廠平均每天用煤噸數y(單位:噸)之間的函數關系;
(2)若平均每天用煤200噸,則這批電煤能用多少天?
(3)若該電廠前10天每天用200噸,后因各地用電緊張,每天用電煤300噸,則這批電煤共可用多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】木匠師傅鋸木料時,一般先在木板上畫出兩個點,然后過這兩點彈出一條墨線,這是因為( )
A. 兩點之間,線段最短
B. 兩點確定一條直線
C. 過一點,有無數條直線
D. 連接兩點之間的線段叫做兩點間的距離
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°.
(1)利用直尺和圓規按下列要求作圖,并在圖中標明相應的字母.(保留作圖痕跡,不寫作法)
①作AC的垂直平分線,交AB于點O,交AC于點D;
②以O為圓心,OA為半徑作圓,交OD的延長線于點E.
(2)在(1)所作的圖形中,解答下列問題.
①點B與⊙O的位置關系是__;(直接寫出答案)
②若DE=2,AC=8,求⊙O的半徑.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,公路AB和公路CD在點P處交會,且∠APC=45°,點Q處有一所小學,PQ=![]() ,假設拖拉機行駛時,周圍130m以內會受到噪聲的影響,那么拖拉機在公路AB上沿PA方向行駛時,學校是否會受到噪聲影響?請說明理由;若受影響,已知拖拉機的速度為36km/h,那么學校受影響的時間為多少秒?
,假設拖拉機行駛時,周圍130m以內會受到噪聲的影響,那么拖拉機在公路AB上沿PA方向行駛時,學校是否會受到噪聲影響?請說明理由;若受影響,已知拖拉機的速度為36km/h,那么學校受影響的時間為多少秒?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖所示,△ABC中,∠BAC=90°,AB=AC,分別過點B、C作經過點A的直線l的垂線段BD、CE,垂足分別D、E.
(1)求證:DE=BD+CE.
(2)如果過點A的直線經過∠BAC的內部,那么上述結論還成立嗎?請畫出圖形,直接給出你的結論(不用證明).
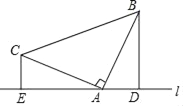
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某經銷店為某工廠代銷一種建筑材料,當每噸售價為260元時,月銷售量為45噸,該經銷店為提高經營利潤,準備采取降價的方式進行促銷,經市場調查發現:當每噸售價下降10元時,月銷售量就會增加7.5噸,綜合考慮各種因素,每售出1噸建筑材料共需支付廠家及其他費用100元,設每噸材料售價為x(元),該經銷店的月利潤為y(元).
①當每噸售價是240元時,計算此時的月銷售量;
②求出y與x的函數關系式(不要求寫出x的取值范圍);
③該經銷店要獲得最大月利潤,售價應定為每噸多少元?
④小靜說:“當月利潤最大時,月銷售額也最大.”你認為對嗎?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com