
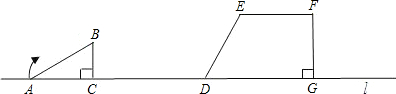
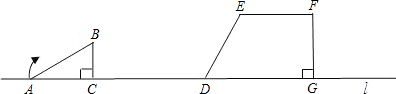
 解:(1)在△ABC中,由已知得:BC=2cm,AC=AB×cos30°=
解:(1)在△ABC中,由已知得:BC=2cm,AC=AB×cos30°= cm,
cm,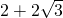 cm.
cm. AB=
AB= ×4=2cm,
×4=2cm,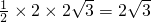 cm2,
cm2, (x-2)
(x-2) (x-2)=
(x-2)= (x-2)2,
(x-2)2, S△ABC=
S△ABC= 時,即
時,即 (x-2)2=
(x-2)2=
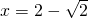 (舍)或x=2+
(舍)或x=2+ .
. cm時,重疊部分的面積等于△ABC的面積的一半.
cm時,重疊部分的面積等于△ABC的面積的一半. cm2.
cm2. (10-x)•
(10-x)• (10-x)=
(10-x)= (10-x)2,
(10-x)2, S△ABC=
S△ABC= 時,即
時,即 (10-x)2=
(10-x)2= ,
, cm,或x=10+
cm,或x=10+ cm(舍去).
cm(舍去). cm時,重疊部分的面積等于△ABC的面積的一半.
cm時,重疊部分的面積等于△ABC的面積的一半. cm或x=10-
cm或x=10- cm時,重疊部分的面積等于△ABC的面積的一半.
cm時,重疊部分的面積等于△ABC的面積的一半.

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
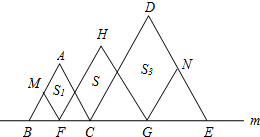 如圖,在直線m上擺放著三個正三角形:△ABC、△HFG、△DCE,已知BC=
如圖,在直線m上擺放著三個正三角形:△ABC、△HFG、△DCE,已知BC=| 1 | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
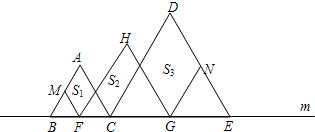 如圖,在直線m上擺放著三個正三角形:△ABC、△HFG、△DCE,已知BC=GE,F、G分別是BC、CE的中點,FM∥AC,GN∥DC.設圖中三個平行四邊形的面積依次是S1,S2,S3,若S1+S3=20,則S2等于( )
如圖,在直線m上擺放著三個正三角形:△ABC、△HFG、△DCE,已知BC=GE,F、G分別是BC、CE的中點,FM∥AC,GN∥DC.設圖中三個平行四邊形的面積依次是S1,S2,S3,若S1+S3=20,則S2等于( )| A、7 | B、8 | C、9 | D、10 |
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 | 2 |
 若S1+S3=10,則S2=
若S1+S3=10,則S2=查看答案和解析>>
科目:初中數學 來源:第2章《二次函數》中考題集(48):2.7 最大面積是多少(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com