
【題目】請閱讀下列材料:
問題:如圖1,在等邊三角形ABC內有一點P,且PA=2,PB=![]() ,PC=1、求∠BPC度數的大小和等邊三角形ABC的邊長.
,PC=1、求∠BPC度數的大小和等邊三角形ABC的邊長.
小剛同學的思路是:將△BPC繞點B逆時針旋轉60°,畫出旋轉后的圖形(如圖2),連接PP′,可得△P′PC是等邊三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可證),所以∠APB=150°,而∠BPC=∠AP′B=150°,進而求出等邊△ABC的邊長為![]() ,問題得到解決.
,問題得到解決.
請你參考小剛同學的思路,探究并解決下列問題:
如圖3,在正方形ABCD內有一點P,且PA=![]() ,BP=2,PC=
,BP=2,PC=![]() .求∠BPC度數的大小和正方形ABCD的邊長.
.求∠BPC度數的大小和正方形ABCD的邊長.
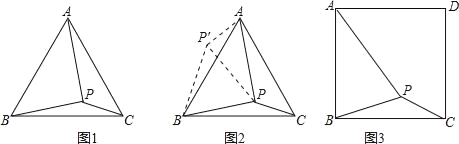
【答案】∠BPC=135°,正方形邊長為![]() .
.
【解析】
首先根據旋轉的性質得出△BPC≌△BP′A,利用AP′=PC=![]() ,BP=BP′=2得出△AP′P是直角三角形,再利用過點B作BE⊥AP′交AP′的延長線于點E,利用勾股定理得出AB的長.
,BP=BP′=2得出△AP′P是直角三角形,再利用過點B作BE⊥AP′交AP′的延長線于點E,利用勾股定理得出AB的長.
解:如圖,將△BPC繞點B逆時針旋轉90°,得△BP′A,
則△BPC≌△BP′A.
∴AP′=PC=![]() ,BP=BP′=2.
,BP=BP′=2.
連結P P′,
在Rt△BP′P中,
∵BP=BP′=2,∠PBP′=90°,
∴P P′=2![]() ,∠BP′P=45°.
,∠BP′P=45°.
在△AP′P中,AP′=![]() ,P P′=2
,P P′=2![]() ,AP=
,AP=![]() ,
,
∵(![]() )2+(2
)2+(2![]() )2=(
)2=(![]() )2,即AP′2+PP′2=AP2.
)2,即AP′2+PP′2=AP2.
∴△AP′P是直角三角形,即∠A P′P=90°.
∴∠AP′B=135°.
∴∠BPC=∠AP′B=135°.
如圖,過點B作BE⊥AP′交AP′的延長線于點E.
∴∠EP′B=45°.
∴EP′=BE=![]() .
.
∴AE=2![]() .
.
∴在Rt△ABE中,由勾股定理,得AB=![]() .
.
∴∠BPC=135°,正方形邊長為![]() .
.


 小學奪冠AB卷系列答案
小學奪冠AB卷系列答案 ABC考王全優卷系列答案
ABC考王全優卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,將![]() 繞點
繞點![]() 順時針旋轉得到
順時針旋轉得到![]() ,使點
,使點![]() 的對應點
的對應點![]() 恰好落在邊
恰好落在邊![]() 上,點
上,點![]() 的對應點為
的對應點為![]() ,連接
,連接![]() ,其中有:①
,其中有:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,四個結論,則結論一定正確的有( )個
,四個結論,則結論一定正確的有( )個
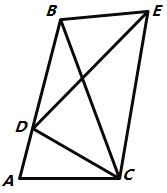
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
(1)若∠BAC=50°,求∠EDA的度數;
(2)求證:直線AD是線段CE的垂直平分線.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班將舉行“數學知識競賽”活動,班長安排小明購買獎品,下面兩圖是小明買回獎品時與班長的對話情境:

請根據上面的信息,解決問題:
(1)試計算兩種筆記本各買了多少本?
(2)請你解釋:小明為什么不可能找回68元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了進一步了解某校初中學生的體質健康狀況,對八年級的部分學生進行了體質監測,同時統計了每個人的得分(假設這個得分為![]() ,滿分為50分).體質檢測的成績分為四個等級:優秀
,滿分為50分).體質檢測的成績分為四個等級:優秀![]() 、良好
、良好![]() 、合格
、合格![]() 、不合格
、不合格![]() .根據調查結果繪制了下列兩福不完整的統計圖,請你根據統計圖提供的信息回答以下問題:
.根據調查結果繪制了下列兩福不完整的統計圖,請你根據統計圖提供的信息回答以下問題:
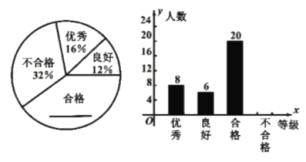
(1)補全上面的扇形統計圖和條形統計圖;
(2)被測試的部分八年級學生的體質測試成績的中位數落在 等級:
(3)若該校八年級有1400名學生,估計該校八年級體質為“不合格”的學生約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,以斜邊AB上一點O為圓心,OB為半徑作⊙O,交AC于點E,交AB于點D,且∠BEC=∠BDE.
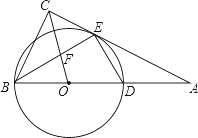
(1)求證:AC是⊙O的切線;
(2)連接OC交BE于點F,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
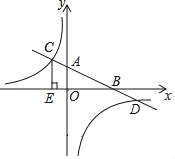
【題目】已知:如圖,在平面直角坐標系xOy中,直線AB分別與x軸、y軸交于點B,A,與反比例函數的圖象分別交于點C,D,CE⊥x軸于點E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求該反比例函數的解析式;
(2)求三角形CDE的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com