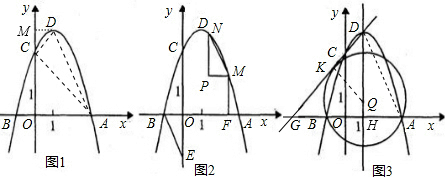
解:(1)把B(-1,0)代入得:b=3a,
y=ax
2-2ax-3a=a(x-1)
2-4a,
所以頂點D(1,-4a).
(2)①有題設知:點C(0,-3a),點A(3,0),
且∠ACD=90°;
在Rt△AOC中,AC
2=9a
2+3
2,
在Rt△AHD中,AD
2=16a
2+2
2,
在Rt△CMD中,CD
2=a
2+1
2,
因為AD
2=AC
2+CD
2,
所以16a
2+2
2=a
2+1
2+9a
2+3
2,a
2=1,又a<0,
所以a=-1,
拋物線的解析式為y=-x
2+2x+3.
②設點M(m,y
1)
則BF=m+1,
點MF:BF=1:2,
∴MF=

,即y
1=

點M(m,y
1)在拋物線上,
所以

=-m
2+2m+3,
解得:m=

或m=-1(舍去),
點M的坐標為M(

,

);
又因為MP∥BO,MP=BO,
所以點的坐標為P(

,

),
由

得點N的坐標為N(

,

).
③設點Q(1,y)
因為D(1,4),C(0,3)
直線CD的方程為y=x+3,
令y=0,得G(-3,0),
設直線CD與⊙O的切點為K,連接QK;
則△DQK∽△DGH,
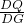
=
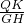
,
又QK=QB=
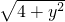
,DQ=4-y,
所以
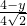
=
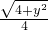
,
整理得:y
2+8y-8=0,
解得y=-4±2

;
所以點Q的坐標為(1,-4+2

)或(1,-4-2

).
說明:由∠QDK=45°,直接得出QD=

QK,從而得4-y=
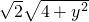
再求解,同樣給分.
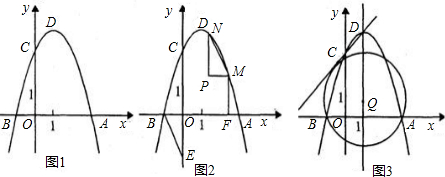
分析:(1)將B點坐標代入拋物線的解析式中,可得到a、b的關系式,將a替換b后,將拋物線的解析式化為頂點坐標式,即可得到頂點D的坐標.
(2)①根據(1)題所得拋物線解析式,可用得到C、A的坐標,若以AD為直徑的圓經過點C,由圓周角定理可知∠ACD=90°,分別用a表示出AC、AD、CD的長,根據勾股定理可得到關于a的方程,即可求出a的值,進而確定該拋物線的解析式.
②根據①題拋物線的解析式,可求得點B的坐標,先設出點M的坐標,可用其橫坐標表示出BF的長,已知BF=2MF,即可得到M點縱坐標的表達式,將其代入拋物線的解析式中,即可得到點M的坐標;根據中心對稱圖形的性質知MP=BO,由此可求得點P(即點N)的橫坐標,將其代入拋物線的解析式中,即可得到點N的坐標.
③若⊙Q與直線CD相切(設切點為K),那么QK=QB=QA,可設出點Q的坐標(橫坐標已知,只設縱坐標即可),可表示出QB、QK、DQ的長;設直線DC與x軸的交點為G,易求得直線DC的解析式,進而可得到點G的坐標,由此可求得HG、DG的長(H為拋物線對稱軸與x軸交點),由于直線CD切⊙Q于點K,易證得△DQK∽△DGH,根據拋物線所得比例線段,即可得到關于點Q縱坐標的方程,通過解方程可確定點Q的坐標.
點評:此題考查了二次函數解析式的確定、圓周角定理、勾股定理、相似三角形的判定和性質以及中心對稱圖形的性質、直線與圓的位置關系等重要知識,涉及知識面廣,難度較大.

 解:(1)把B(-1,0)代入得:b=3a,
解:(1)把B(-1,0)代入得:b=3a, ,即y1=
,即y1=
 =-m2+2m+3,
=-m2+2m+3, 或m=-1(舍去),
或m=-1(舍去), ,
, );
); ,
, ),
), 得點N的坐標為N(
得點N的坐標為N( ,
, ).
).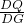 =
=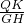 ,
,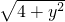 ,DQ=4-y,
,DQ=4-y,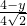 =
=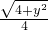 ,
, ;
; )或(1,-4-2
)或(1,-4-2 ).
). QK,從而得4-y=
QK,從而得4-y=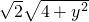 再求解,同樣給分.
再求解,同樣給分.

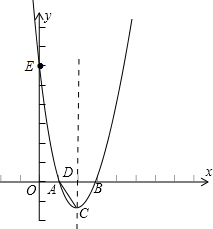 已知二次函數的圖象是經過點A(1,0),B(3,0),E(0,6)三點的一條拋物線.
已知二次函數的圖象是經過點A(1,0),B(3,0),E(0,6)三點的一條拋物線. 閱讀材料:如圖1,過△ABC的三個頂點分別作出與水平線垂直的三條直線,外側兩條直線之間的距離叫△ABC的“水平寬”(a),中間的這條直線在△ABC內部線段的長度叫△ABC的“鉛垂高”(h).我們可得出一種計算三角形面積的新方法:S△ABC=
閱讀材料:如圖1,過△ABC的三個頂點分別作出與水平線垂直的三條直線,外側兩條直線之間的距離叫△ABC的“水平寬”(a),中間的這條直線在△ABC內部線段的長度叫△ABC的“鉛垂高”(h).我們可得出一種計算三角形面積的新方法:S△ABC=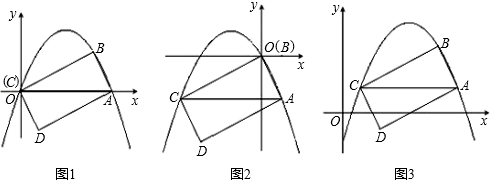
 如圖,將拋物線y=-
如圖,將拋物線y=-