
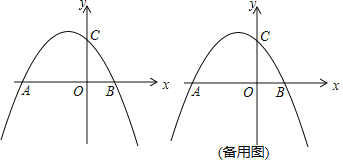
【題目】如圖,二次函數![]() 的圖象與
的圖象與![]() 軸交于點A、B,與y軸交于點C,點A的坐標為(-4,0),P是拋物線上一點 (點P與點A、B、C不重合).
軸交于點A、B,與y軸交于點C,點A的坐標為(-4,0),P是拋物線上一點 (點P與點A、B、C不重合).
(1)b= ,點B的坐標是 ;
(2)設直線PB直線AC交于點M,是否存在這樣的點P,使得PM:MB=1:2?若存在,求出點P的橫坐標;若不存在,請說明理由;
(3)連接AC、BC,判斷∠CAB和∠CBA的數量關系,并說明理由.
【答案】(1)![]() ;(
;(![]() ,0);(2)存在點P的橫坐標為
,0);(2)存在點P的橫坐標為![]() 或
或![]() .(3)∠CBA=2∠CAB.理由見解析.
.(3)∠CBA=2∠CAB.理由見解析.
【解析】
(1)由點A的坐標,利用二次函數圖象上點的坐標特征可求出b的值,代入y=0求出x值,進而可得出點B的坐標;
(2)(解法一)代入x=0求出y值,進而可得出點C的坐標,由點A、C的坐標利用待定系數法可求出直線AC的解析式,假設存在,設點M的坐標為(m,![]() m+2),分B、P在直線AC的同側和異側兩種情況考慮,由點B、M的坐標結合PM:MB=1:2即可得出點P的坐標,再利用二次函數圖象上點的坐標特征可得出關于m的一元二次方程,解之即可得出結論;
m+2),分B、P在直線AC的同側和異側兩種情況考慮,由點B、M的坐標結合PM:MB=1:2即可得出點P的坐標,再利用二次函數圖象上點的坐標特征可得出關于m的一元二次方程,解之即可得出結論;
(解法二)代入x=0求出y值,進而可得出點C的坐標,由點A、C的坐標利用待定系數法可求出直線AC的解析式,過點B作BB′∥y軸交直線AC于點B′,過點P作PP′∥y軸交直線AC于點P′,由點B的坐標可得出BB′的值,結合相似三角形的性質可得出PP′的值,設點P的坐標為(x,-![]() x2-
x2-![]() x+2),則點P′的坐標為(x,
x+2),則點P′的坐標為(x,![]() x+2),結合PP′的值可得出關于x的含絕對值符號的一元二次方程,解之即可得出結論;
x+2),結合PP′的值可得出關于x的含絕對值符號的一元二次方程,解之即可得出結論;
(3)作∠CBA的角平分線,交y軸于點E,過點E作EF⊥BC于點F,設OE=n,則CE=2-n,EF=n,利用面積法可求出n值,進而可得出![]() ,結合∠AOC=90°=∠BOE可證出△AOC∽△BOE,根據相似三角形的性質可得出∠CAO=∠EBO,再根據角平分線的性質可得出∠CBA=2∠EBO=2∠CAB,此題得解.
,結合∠AOC=90°=∠BOE可證出△AOC∽△BOE,根據相似三角形的性質可得出∠CAO=∠EBO,再根據角平分線的性質可得出∠CBA=2∠EBO=2∠CAB,此題得解.
(1)![]() 點
點![]() 在二次函數
在二次函數![]() 的圖象上,
的圖象上,
![]() ,
,
![]() .
.
當![]() 時, 有
時, 有![]() ,
,
解得:![]() ,
,![]() ,
,
![]() 點
點![]() 的坐標為
的坐標為![]() ,
,![]() .
.
故答案為:![]() ;
;![]() ,
,![]() .
.
(2) (方 法一) 當![]() 時,
時,![]() ,
,
![]() 點
點![]() 的坐標為
的坐標為![]() .
.
設直線![]() 的解析式為
的解析式為![]() ,
,
將![]() 、
、![]() 代入
代入![]() 中,
中,
得:![]() ,解得:
,解得:![]() ,
,
![]() 直線
直線![]() 的解析式為
的解析式為![]() .
.
假設存在, 設點![]() 的坐標為
的坐標為![]() .
.
①當點![]() 、
、![]() 在直線
在直線![]() 的異側時, 點
的異側時, 點![]() 的坐標為
的坐標為![]() ,
,![]() ,
,
![]() 點
點![]() 在拋物線
在拋物線![]() 上,
上,
![]()
![]() ,
,
整理, 得:![]() .
.
![]() △
△![]() ,
,
![]() 方程無解, 即不存在符合題意得點
方程無解, 即不存在符合題意得點![]() ;
;
②當點![]() 、
、![]() 在直線
在直線![]() 的同側時, 點
的同側時, 點![]() 的坐標為
的坐標為![]() ,
,![]() ,
,
![]() 點
點![]() 在拋物線
在拋物線![]() 上,
上,
![]()
![]() ,
,
整理, 得:![]() ,
,
解得:![]() ,
,![]() ,
,
![]() 點
點![]() 的橫坐標為
的橫坐標為![]() 或
或![]() .
.
綜上所述: 存在點![]() ,使得
,使得![]() ,點
,點![]() 的橫坐標為
的橫坐標為![]() 或
或![]() .
.
(3)![]() ,理由如下:
,理由如下:
作![]() 的角平分線, 交
的角平分線, 交![]() 軸于點
軸于點![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,如圖 2 所示 .
,如圖 2 所示 .
![]() 點
點![]() ,
,![]() ,點
,點![]() ,
,
![]() ,
,![]() ,
,![]() .
.
設![]() ,則
,則![]() ,
,![]() ,
,
由面積法, 可知:![]() ,即
,即![]() ,
,
解得:![]() .
.
![]()
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.


 名師點撥卷系列答案
名師點撥卷系列答案科目:初中數學 來源: 題型:
【題目】某段筆直的限速公路上,規定汽車的最高行駛速度不能超過60km/h(即![]() m/s),交通管理部門在離該公路100m處設置了一速度檢測點A,在如圖所示的坐標系中,A位于y軸上,測速路段BC在x軸上,點B在A的北偏西60°方向上,點C在點A的北偏東45°方向上.
m/s),交通管理部門在離該公路100m處設置了一速度檢測點A,在如圖所示的坐標系中,A位于y軸上,測速路段BC在x軸上,點B在A的北偏西60°方向上,點C在點A的北偏東45°方向上.
(1)在圖中直接標出表示60°和45°的角;
(2)寫出點B、點C坐標;
(3)一輛汽車從點B勻速行駛到點C所用時間為15s.請你通過計算,判斷該汽車在這段限速路上是否超速?(本小問中![]() 取1.7)
取1.7)

查看答案和解析>>
科目:初中數學 來源: 題型:
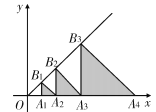
【題目】如圖,在平面直角坐標系中,點A1,A2,A3…都在x軸上,點B1,B2,B3…都在直線y=x上,OA1=1,且△B1A1A2,△B2A2A3,△B3A3A4,…△Bn A n A n+1…分別是以A1,A2,A3,…An…為直角頂點的等腰直角三角形,則△B10A10A11的面積是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
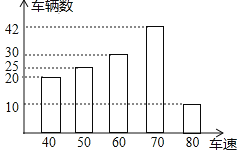
【題目】為了了解一路段車輛行駛速度的情況,交警統計了該路段上午7::0至9:00來往車輛的車速(單位:千米/時),并繪制成如圖所示的條形統計圖.這些車速的眾數、中位數分別是( )
A. 眾數是80千米![]() 時,中位數是60千米
時,中位數是60千米![]() 時
時
B. 眾數是70千米![]() 時,中位數是70千米
時,中位數是70千米![]() 時
時
C. 眾數是60千米![]() 時,中位數是60千米
時,中位數是60千米![]() 時
時
D. 眾數是70千米![]() 時,中位數是60千米
時,中位數是60千米![]() 時
時
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某市初中學生課外閱讀情況,調查小組對該市這學期初中學生閱讀課外書籍的冊數進行了抽樣調查,并根據調查結果繪制成如下統計圖.
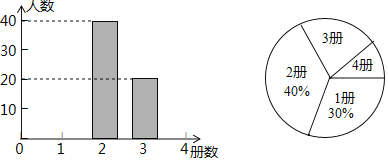
根據統計圖提供的信息,解答下列問題:
(1)本次抽樣調查的樣本容量是 ;
(2)補全條形統計圖;
(3)該市共有12000名初中生,估計該市初中學生這學期課外閱讀超過2冊的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,已知拋物線y=![]() +bx﹣4經過A(﹣4,0),C(2,0)兩點.
+bx﹣4經過A(﹣4,0),C(2,0)兩點.
(1)求拋物線的解析式;
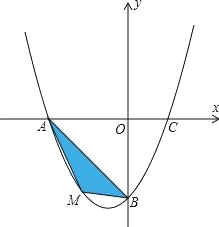
(2)若點M為第三象限內拋物線上一動點,點M的橫坐標為m,△AMB的面積為S.求S關于m的函數關系式,并求出S的最大值;
(3)若點P是拋物線上的動點,點Q是直線y=﹣x上的動點,點B是拋物線與y軸交點.判斷有幾個位置能夠使以點P、Q、B、O為頂點的四邊形為平行四邊形,直接寫出相應的點Q的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
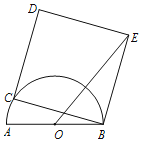
【題目】如圖,點C是半圓![]() 上一動點,以BC為邊作正方形BCDE,使
上一動點,以BC為邊作正方形BCDE,使![]() 在正方形內,連OE,若AB=4cm,則OD的最大值為_____________cm.
在正方形內,連OE,若AB=4cm,則OD的最大值為_____________cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】反比例函數y=![]() 和y=
和y=![]() 在第一象限內的圖象如圖所示,點P在y=
在第一象限內的圖象如圖所示,點P在y=![]() 的圖象上,PC⊥x軸,交y=
的圖象上,PC⊥x軸,交y=![]() 的圖象于點A,PD⊥y軸,交y=
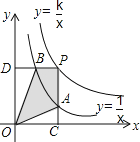
的圖象于點A,PD⊥y軸,交y=![]() 的圖象于點B.當點P在y=
的圖象于點B.當點P在y=![]() 的圖象上運動時,以下結論:①△ODB與△OCA的面積相等;②PA與PB始終相等;③四邊形PAOB的面積不會發生變化;④當點A是PC的中點時,點B一定是PD的中點.其中一定正確的是( )
的圖象上運動時,以下結論:①△ODB與△OCA的面積相等;②PA與PB始終相等;③四邊形PAOB的面積不會發生變化;④當點A是PC的中點時,點B一定是PD的中點.其中一定正確的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,∠A=110°,E,F分別是邊AB和BC的中點,EP⊥CD于點P,則∠FPC=( )
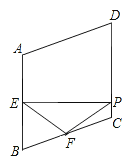
A. 35° B. 45° C. 50° D. 55°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com