
【題目】已知a是最大的負整數,b是-5的相反數,c=![]() ,且a、b、c分別是點A、B、C在數軸上對應的數.若動點P從點A出發沿數軸正方向運動,動點Q同時從點B出發也沿數軸正方向運動,點P的速度是每秒3個單位長度,點Q的速度是每秒1個單位長度.
,且a、b、c分別是點A、B、C在數軸上對應的數.若動點P從點A出發沿數軸正方向運動,動點Q同時從點B出發也沿數軸正方向運動,點P的速度是每秒3個單位長度,點Q的速度是每秒1個單位長度.
![]()
(1)求a、b、c的值;
(2)P、Q同時出發,求運動幾秒后,點P可以追上點Q?
(3)在(2)的條件下,P、Q出發的同時,動點M從點C出發沿數軸正方向運動,速度為每秒6個單位長度,點M追上點Q后立即返回沿數軸負方向運動,追上后點M再運動幾秒,M到Q的距離等于M到P距離的兩倍?
【答案】(1)a=-1,b=5,c=-3;(2)t=3s;(3)t=![]() 或
或![]() s
s
【解析】
(1)由已知條件即可確定a、b、c的值;
(2)由題意,可知A點表示的數是-1,B點表示的數是5,設運動t秒后,P點對應的數是-1+3t,Q點對應的數是5+t,相遇時兩點表示同一個數;
(3),t秒后,M點對應的數是-3+6t,可求M、Q相遇時間,當M向數軸負半軸運動后,M點對應的數是6.6-6(t-1.6)=-6t+16.2,根據題意列出方程7t-11.2=2|9t-17.2|,再結合t的范圍求解.
解:(1)∵a是最大的負整數,
∴a=-1,
∵b是-5的相反數,
∴b=5,
∵c=-|-3|,
∴c=-3;
(2)由題意,可知A點表示的數是-1,B點表示的數是5,
設運動t秒后,P點對應的數是-1+3t,Q點對應的數是5+t,
P點追上Q點時,兩個點表示的數相同,
∴-1+3t=5+t,
∴t=3,
∴求運動3秒后,點P可以追上點Q;
(3)由(2)知,t秒后,M點對應的數是-3+6t,
當M點追上Q點時,5+t=-3+6t,
∴t=1.6,
此時M點對應的數是6.6,
此后M點向數軸負半軸運動,M點對應的數是6.6-6(t-1.6)=-6t+16.2,
MQ=5+t-(-6t+16.2)=7t-11.2,
MP=|-6t+16.2+1-3t|=|9t-17.2|,
由題意,可得7t-11.2=2|9t-17.2|,
當![]() 時,7t-11.2=18t-34.4,
時,7t-11.2=18t-34.4,
∴t=![]()
當![]() 時,7t-11.2=-18t+34.4,
時,7t-11.2=-18t+34.4,
∴t=![]() ;
;
∴t=![]() 或t=
或t=![]() ,
,
∴![]() ,
,![]() ,
,
∴追上后,再經過![]() s或
s或![]() s,M到Q的距離等于M到P距離的兩倍.
s,M到Q的距離等于M到P距離的兩倍.


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:初中數學 來源: 題型:
【題目】已知數a在數軸上表示的點在原點左側,距離原點3個單位長,b在數軸上表示的點在原點右側,距離原點2個單位長,c和d互為倒數,m與n互為相反數,y為最大的負整數,求(y+b)2+m(a-cd)-nb2的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】廣州火車南站廣場計劃在廣場內種植A,B兩種花木共 6600棵,若A花木數量是B花木數量的2倍少600棵.
(1)A,B兩種花木的數量分別是多少棵?
(2)如果園林處安排26人同時種植這兩種花木,每人每天能種植A花木60棵或B花木40棵,應分別安排多少人種植A花木和B花木,才能確保同時完成各自的任務?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,過A(1,0)、B(3,0)作x軸的垂線,分別交直線y=﹣x+4于C、D兩點.拋物線y=ax2+bx+c經過O、C、D三點.

(1)求拋物線的表達式;
(2)點M為直線OD上的一個動點,過M作x軸的垂線交拋物線于點N,問是否存在這樣的點M,使得以A、C、M、N為頂點的四邊形為平行四邊形?若存在,求此時點M的橫坐標;若不存在,請說明理由;
(3)若△AOC沿CD方向平移(點C在線段CD上,且不與點D重合),在平移的過程中△AOC與△OBD重疊部分的面積記為S,試求S的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用正方形硬紙板做三棱柱盒子,每個盒子由3個矩形側面和2個正三角形底面組成。硬紙板以如圖兩種方式裁剪(裁剪后邊角料不再利用)
A方法:剪6個側面; B方法:剪4個側面和5個底面。

現有19張硬紙板,裁剪時![]() 張用A方法,其余用B方法。
張用A方法,其余用B方法。
(1)用![]() 的代數式分別表示裁剪出的側面和底面的個數;
的代數式分別表示裁剪出的側面和底面的個數;
(2)若裁剪出的側面和底面恰好全部用完,問能做多少個盒子?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:
數軸上線段的長度可以用線段端點表示的數進行減法運算得到,例如圖,線段AB=1=0﹣(﹣1);線段 BC=2=2﹣0;線段 AC=3=2﹣(﹣1)問題
①數軸上點M、N代表的數分別為﹣9和1,則線段MN= ;
②數軸上點E、F代表的數分別為﹣6和﹣3,則線段EF= ;
③數軸上的兩個點之間的距離為5,其中一個點表示的數為2,則另一個點表示的數為m,求m.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() =
=![]() (
(![]() ≠0)與
≠0)與![]() 軸交于AB兩點,與
軸交于AB兩點,與![]() 軸交于C點,其對稱軸為
軸交于C點,其對稱軸為![]() =1,且A(-1,0)C(0,2).
=1,且A(-1,0)C(0,2).
(1)直接寫出該拋物線的解析式;
(2)P是對稱軸上一點,△PAC的周長存在最大值還是最小值?請求出取得最值(最大值或最小值)時點P的坐標;
(3)設對稱軸與![]() 軸交于點H,點D為線段CH上的一動點(不與點CH重合).點P是(2)中所求的點.過點D作DE∥PC交
軸交于點H,點D為線段CH上的一動點(不與點CH重合).點P是(2)中所求的點.過點D作DE∥PC交![]() 軸于點E.連接PDPE.若CD的長為
軸于點E.連接PDPE.若CD的長為![]() ,△PDE的面積為S,求S與
,△PDE的面積為S,求S與![]() 之間的函數關系式,試說明S是否存在最值,若存在,請求出最值,并寫出S取得的最值及此時
之間的函數關系式,試說明S是否存在最值,若存在,請求出最值,并寫出S取得的最值及此時![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
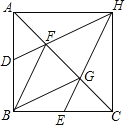
【題目】已知:如圖,在△ABC中,AB=BC,∠ABC=90°,點D、E分別是邊AB、BC的中點,點F、G是邊AC的三等分點,DF、EG的延長線相交于點H,連接HA、HC.
(1)求證:四邊形FBGH是菱形;
(2)求證:四邊形ABCH是正方形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點![]() ,
,![]() 在數軸上分別表示有理數
在數軸上分別表示有理數![]() ,
,![]() ,
,![]() ,
,![]() 兩點之間的距離表示為
兩點之間的距離表示為![]() ,在數軸上
,在數軸上![]() ,
,![]() 兩點之間的距離
兩點之間的距離![]() .已知數軸上
.已知數軸上![]() ,
,![]() 兩點表示數
兩點表示數![]() ,
,![]() 滿足
滿足![]() ,點
,點![]() 為數軸上一動點,其對應的數為
為數軸上一動點,其對應的數為![]() .
.
![]()
(1)![]() ,
,![]() 兩點之間的距離是.
兩點之間的距離是.
(2)![]() 與
與![]() 之間的距離表示為.
之間的距離表示為.
(3)數軸上是否存在點![]() ,使點
,使點![]() 到點
到點![]() ,點
,點![]() 的距離之和為
的距離之和為![]() ?若存在,請求出
?若存在,請求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
(4)現在點![]() ,點
,點![]() 分別以
分別以![]() 單位/秒和
單位/秒和![]() 單位/秒的速度同時向右運動,當點
單位/秒的速度同時向右運動,當點![]() 與點
與點![]() 之間的距離為
之間的距離為![]() 個單位長度時,求點
個單位長度時,求點![]() 所對應的數是多少?
所對應的數是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com