
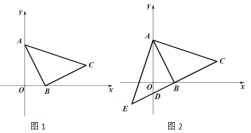
【題目】如圖1:已知直線![]() 與
與![]() 軸,
軸,![]() 軸分別交于
軸分別交于![]() ,
,![]() 兩點,以
兩點,以![]() 為直角頂點在第一象限內做等腰Rt△
為直角頂點在第一象限內做等腰Rt△![]() .
.
(1)求![]() ,
,![]() 兩點的坐標;
兩點的坐標;
(2)求![]() 所在直線的函數關系式;
所在直線的函數關系式;
(3)如圖2,直線![]() 交
交![]() 軸于點
軸于點![]() ,在直線
,在直線![]() 上存在一點
上存在一點![]() ,使
,使![]() 是△
是△![]() 的中線,求點E的坐標.
的中線,求點E的坐標.
【答案】(1)A(0,2),B(1,0);(2)![]() ;(3)E的坐標是(-1,-1)
;(3)E的坐標是(-1,-1)
【解析】
(1)y=-2x+2中求出x=0時y的值和y=0時x的值即可得;
(2)作CD⊥x軸,證△ABO≌△BCD得BD=OA=2,CD=OB=1,據此可得C(3,1),再根據待定系數法求解可得;(3)過點E作![]() 軸于點F,由
軸于點F,由![]() 是△
是△![]() 的中線得DE=BD,然后證明
的中線得DE=BD,然后證明![]() ,進而得到EF=OB,OD=DF=
,進而得到EF=OB,OD=DF=![]() ,從而求解.
,從而求解.
解:(1)y=-2x+2中,當x=0時y=2,
則A(0,2),
當y=0時,-2x+2=0,解得x=1,
則B(1,0);
(2)如圖①,過點C作CD⊥x軸于點D,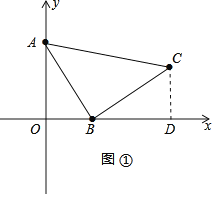
則∠AOB=∠BDC=90°,
∴∠OAB+∠ABO=90°,
∵△ABC是等腰直角三角形,
∴AB=BC,∠ABC=90°,
∴∠ABO+∠CBD=90°,
∴∠OAB=∠DBC,
∴△ABO≌△BCD(AAS),
∴BD=OA=2,CD=OB=1,
則點C(3,1),
設直線BC所在直線解析式為y=kx+b,
將點B(1,0)、C(3,1)代入,得:![]() ,
,
解得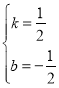 ,
,
∴直線BC所在直線解析式為![]() .
.
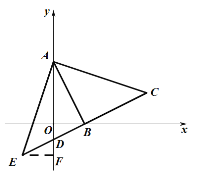
(3)過點E作![]() 軸于點F
軸于點F
∵![]() 是△
是△![]() 的中線
的中線
∴ DE=BD
![]() 軸
軸
![]()
![]()
EF=OB,OD=DF=![]()
點E的坐標是(-1,-1)


科目:初中數學 來源: 題型:
【題目】已知方程![]() 的兩個根是
的兩個根是![]() ,那么
,那么![]() ,反過來,如果
,反過來,如果![]() ,那么以
,那么以![]() 為兩根的一元二次方程是
為兩根的一元二次方程是![]() .請根據以上結論,解決下列問題:
.請根據以上結論,解決下列問題:
(1)已知關于x的方程![]() +mx+n=0(n≠0),求出—個一元二次方程,使它的兩根分別是已知方程兩根的倒數.
+mx+n=0(n≠0),求出—個一元二次方程,使它的兩根分別是已知方程兩根的倒數.
(2)已知a、b滿足![]() -15a-5=0,
-15a-5=0,![]() -15b-5=0,求
-15b-5=0,求![]() 的值.
的值.
(3)已知a、b、c均為實數,且a+b+c=0,abc=16,求正數C的最小值
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學課上,李老師出示了如下框中的題目.
在等邊三角形ABC中,點E在AB上,點D在CB的延長線上,且ED=EC,如圖.試確定線段AE與DB的大小關系,并說明理由. |
|
小敏與同桌小聰討論后,進行了如下解答:
(1)特殊情況,探索結論
當點E為AB的中點時,如圖1,確定線段AE與的DB大小關系.請你直接寫出結論:
AE DB(填“>”,“<”或“=”).

圖1 圖2
(2)特例啟發,解答題目
解:題目中,AE與DB的大小關系是:AE DB(填“>”,“<”或“=”).
理由如下:如圖2,過點E作EF∥BC,交AC于點F.
(請你完成以下解答過程)
(3)拓展結論,設計新題
在等邊三角形ABC中,點E在直線AB上,點D在直線BC上,且ED=EC.若△ABC的邊長為1,AE=2,求CD的長(請你直接寫出結果).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線![]() 是第一、三象限的角平分線.
是第一、三象限的角平分線.
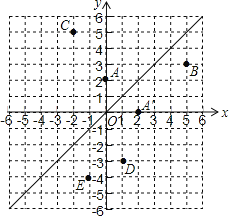
(1)由圖觀察易知A(0,2)關于直線l的對稱點A′的坐標為(2,0),請在圖中分別標明B(5,3)、C(-2,5)關于直線l的對稱點B′、C′的位置,并寫出他們的坐標:![]() ___________、
___________、![]() ___________;
___________;
(2)結合圖形觀察以上三組點的坐標,你會發現:坐標平面內任一點![]() 關于第一、三象限的角平分線
關于第一、三象限的角平分線![]() 的對稱點
的對稱點![]() 的坐標為___________(不必證明);
的坐標為___________(不必證明);
(3)已知兩點![]() 、
、![]() ,試在直線L上畫出點Q,使點Q到D、E兩點的距離之和最小,求QD+QE的最小值.
,試在直線L上畫出點Q,使點Q到D、E兩點的距離之和最小,求QD+QE的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線y=kx+b交x軸于點A,交y軸于點B,直線y=2x﹣4交x軸于點D,與直線AB相交于點C(3,2).
(1)根據圖象,寫出關于x的不等式2x﹣4>kx+b的解集;
(2)若點A的坐標為(5,0),求直線AB的解析式;
(3)在(2)的條件下,求四邊形BODC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,已知拋物線y=ax2+bx+3(a≠0)與x軸交于點A(1,0)和點B(﹣3,0),與y軸交于點C.
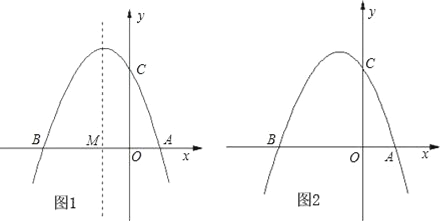
(1)求拋物線的解析式;
(2)設拋物線的對稱軸與x軸交于點M,問在對稱軸上是否存在點P,使△CMP為等腰三角形?若存在,請直接寫出所有符合條件的點P的坐標;若不存在,請說明理由;
(3)如圖②,若點E為第二象限拋物線上一動點,連接BE、CE,求四邊形BOCE面積的最大值,并求此時E點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() ,
,![]() 兩種機器人都被用來搬運化工原料,
兩種機器人都被用來搬運化工原料,![]() 型機器人每小時搬運的化工原料是
型機器人每小時搬運的化工原料是![]() 型機器人每小時搬運的化工原料的1.5倍,
型機器人每小時搬運的化工原料的1.5倍,![]() 型機器人搬運900
型機器人搬運900![]() 所用時間比
所用時間比![]() 型機器人搬運800
型機器人搬運800![]() 所用時間少1小時.
所用時間少1小時.
(1)求兩種機器人每小時分別搬運多少化工原料?
(2)某化工廠有8000![]() 化工原料需要搬運,要求搬運所有化工原料的時間不超過5小時,現計劃先由6個
化工原料需要搬運,要求搬運所有化工原料的時間不超過5小時,現計劃先由6個![]() 型機器人搬運3小時,再增加若干個
型機器人搬運3小時,再增加若干個![]() 型機器人一起搬運,請問至少要增加多少個
型機器人一起搬運,請問至少要增加多少個![]() 型機器人?
型機器人?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com