
 分別交x軸、y軸于B、A兩點,拋物線L:y=ax2+bx+c的頂點G在x軸上,且過(0,4)和(4,4)兩點。
分別交x軸、y軸于B、A兩點,拋物線L:y=ax2+bx+c的頂點G在x軸上,且過(0,4)和(4,4)兩點。
| 解:(1)∵拋物線L過(0,4)和(4,4)兩點,由拋物線的對稱性知對稱軸為x=2 ∴G(2,0),將(2,0)、(4,4)代入  , ,得  ,解得 ,解得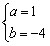 ∴拋物線L的解析式為 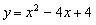 。 。(2)∵直線  分別交x軸、y軸于B、A兩點, 分別交x軸、y軸于B、A兩點,∴A(0,3),B(-  ,0) ,0)若拋物線L上存在滿足的點C,則AC∥BG, ∴C點縱坐標此為3,設C(m,3), 又C在拋物線L,代入解析式: 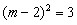 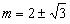 ∴ 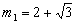 , ,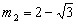 當 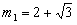 時,BG= 時,BG=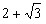 ,AG= ,AG= ∴BG∥AG且BG=AG,此時四邊形ABGC是平行四邊形,舍去 當 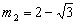 時, 時,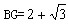 , , ∴BG∥AG且BG≠AG,此時四邊形ABGC是梯形 故存在這樣的點C,使得四邊形ABGC是以BG為底邊的梯形, 其坐標為:C( 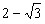 ,3)。 ,3)。 |
|
(3)假設拋物線L1是存在的,且對應的函數關系式為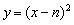 ∴頂點P(n,0) Rt△ABO中,AO=3,BO= 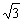 ,可得∠ABO=60°, ,可得∠ABO=60°,又△ABD≌△ABP ∴∠ABD=60°,BD=BP= 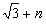 如圖,過D作DN⊥軸于N點, Rt△BND中,BD= 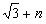 ,∠DBN=60° ,∠DBN=60°∴ 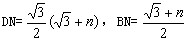 ∴D( 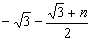 , ,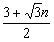 ) )即 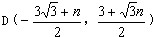 又D點在拋物線 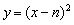 上 上∴ 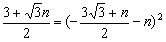 整理得 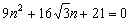 解得 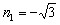 , ,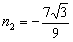 當 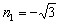 時,P與B重合,不能構成三角形,舍去, 時,P與B重合,不能構成三角形,舍去, ∴當  時,此時拋物線為 時,此時拋物線為 。 。 |
 |


科目:初中數學 來源: 題型:
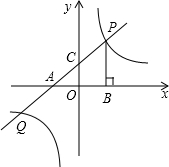 曲線y=
曲線y=| k | x |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,直線l分別交x軸、y軸于A、B兩點,且A(3
如圖,直線l分別交x軸、y軸于A、B兩點,且A(3| 3 |
| 3 |
3
| ||
| 2 |
查看答案和解析>>
科目:初中數學 來源:2010-2011學年北京市順義區李橋中學九年級(上)第三次月考數學試卷(解析版) 題型:解答題
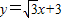 分別交x軸、y軸于B、A兩點,拋物線L:y=ax2+bx+c的頂點G在x軸上,且過(0,4)和(4,4)兩點.
分別交x軸、y軸于B、A兩點,拋物線L:y=ax2+bx+c的頂點G在x軸上,且過(0,4)和(4,4)兩點.
查看答案和解析>>
科目:初中數學 來源:2006年湖北省咸寧市中考數學試卷(解析版) 題型:解答題
 x+1分別交x軸,y軸于點A,C,點P是直線AC與雙曲線y=
x+1分別交x軸,y軸于點A,C,點P是直線AC與雙曲線y= 在第一象限內的交點,PB⊥x軸,垂足為點B,△APB的面積為4.
在第一象限內的交點,PB⊥x軸,垂足為點B,△APB的面積為4.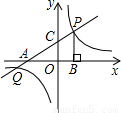
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com