
【題目】綜合題。
(1)(﹣2)﹣1﹣|﹣ ![]() |+(3.14﹣π)0+4cos45°
|+(3.14﹣π)0+4cos45°
(2)已知x2﹣2x﹣7=0,求(x﹣2)2+(x+3)(x﹣3)的值.
【答案】
(1)
解:原式=﹣ ![]() ﹣2
﹣2 ![]() +1+2
+1+2 ![]() =
= ![]()
(2)
解:原式=x2﹣4x+4+x2﹣9=2x2﹣4x﹣5=2(x2﹣2x)﹣5,
∵x2﹣2x﹣7=0,即x2﹣2x=7,
∴原式=14﹣5=9
【解析】(1)原式利用零指數冪、負整數指數冪法則,絕對值的代數意義,以及特殊角的三角函數值計算即可得到結果;(2)原式利用完全平方公式,平方差公式化簡,去括號整理后,將已知等式變形后代入計算即可求出值.
【考點精析】解答此題的關鍵在于理解絕對值的相關知識,掌握正數的絕對值是其本身,0的絕對值是0,負數的絕對值是它的相反數;注意:絕對值的意義是數軸上表示某數的點離開原點的距離,以及對特殊角的三角函數值的理解,了解分母口訣:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口訣:“123,321,三九二十七”.


 新課標同步訓練系列答案
新課標同步訓練系列答案 一線名師口算應用題天天練一本全系列答案
一線名師口算應用題天天練一本全系列答案科目:初中數學 來源: 題型:
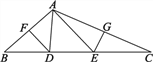
【題目】如圖,△ABC中,∠BAC=110°,AB的垂直平分線交BC于點D,AC的垂直平分線交BC于點E,BC=10cm.求:
(1)△ADE的周長;
(2)∠DAE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
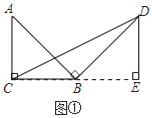
【題目】問題原型:如圖①,在等腰直角三角形ABC中,∠ACB=90°,BC=a.將邊AB繞點B順時針旋轉90°得到線段BD,連結CD.過點D作△BCD的BC邊上的高DE, 易證△ABC≌△BDE,從而得到△BCD的面積為![]() .
.
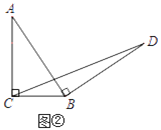
初步探究:如圖②,在Rt△ABC中,∠ACB=90°,BC=a.將邊AB繞點B順時針旋轉90°得到線段BD,連結CD.用含a的代數式表示△BCD的面積,并說明理由.
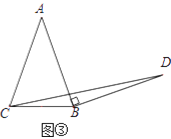
簡單應用:如圖③,在等腰三角形ABC中,AB=AC,BC=a.將邊AB繞點B順時針旋轉90°得到線段BD,連結CD.直接寫出△BCD的面積.(用含a的代數式表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“十一”黃金周期間,歡歡一家隨旅游團到某風景區旅游,集體門票的收費標準是: ![]() 人以內(含
人以內(含![]() 人),每人
人),每人![]() 元;超過
元;超過![]() 人的,超過的部分每人
人的,超過的部分每人![]() 元.
元.
(![]() )寫出應收門票費
)寫出應收門票費![]() (元)與游覽人數
(元)與游覽人數![]() (人)(其中
(人)(其中![]() )之間的關系式.
)之間的關系式.
(![]() )利用(
)利用(![]() )中的關系式計算:若歡歡一家所在的旅游團共
)中的關系式計算:若歡歡一家所在的旅游團共![]() 人,那么該旅游團購門票共花了多少錢?
人,那么該旅游團購門票共花了多少錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等邊三角形ABC中,已知點O是三個內角平分線的交點,OD∥AB,OE∥AC,則圖中等腰三角形的個數是( )
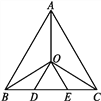
A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=AC,∠BAC=90°,點D在射線BC上(與B、C兩點不重合),以AD為邊作正方形ADEF,使點E與點B在直線AD的異側,射線BA與射線CF相交于點G.
(1)若點D在線段BC上,如圖1.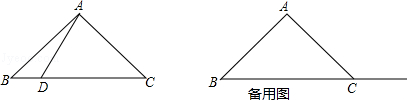
①依題意補全圖1;
②判斷BC與CG的數量關系與位置關系,并加以證明;
(2)若點D在線段BC的延長線上,且G為CF中點,連接GE,AB= ![]() ,則GE的長為
,則GE的長為 ![]() ,并簡述求GE長的思路.
,并簡述求GE長的思路.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校實行學案式教學,需印制若干份教學學案.印刷廠有,甲、乙兩種收費方式,除按印數收取印刷費外,甲種方式還需收取制版費而乙種不需要,兩種印刷方式的費用y(元)與印刷份數x(份)之間的關系如圖所示.

(1)填空:甲種收費方式的函數關系式是__________,乙種收費方式的函數關系式是__________.
(2)該校某年級每次需印制100~450(含100和450)份學案,選擇哪種印刷方式較合算.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計劃撥款9萬元從廠家購進50臺電視機![]() 已知該廠家生產三種不同型號的電視機,出廠價分別為:甲種每臺1500元,乙種每臺2100元,丙種每臺2500元.
已知該廠家生產三種不同型號的電視機,出廠價分別為:甲種每臺1500元,乙種每臺2100元,丙種每臺2500元.
![]() 若商場同時購進其中兩種不同型號電視機共50臺,用去9萬元,請研究一下商場的進貨方案;
若商場同時購進其中兩種不同型號電視機共50臺,用去9萬元,請研究一下商場的進貨方案;
![]() 若商場銷售一臺甲種電視機可獲利150元,銷售一臺乙種電視機可獲利200元,銷售一臺丙種電視機可獲利250元
若商場銷售一臺甲種電視機可獲利150元,銷售一臺乙種電視機可獲利200元,銷售一臺丙種電視機可獲利250元![]() 在同時購進兩種不同型號電視機的方案中,為使銷售時獲利最多,你選擇哪種進貨方案;
在同時購進兩種不同型號電視機的方案中,為使銷售時獲利最多,你選擇哪種進貨方案;
![]() 若商場準備用9萬元同時購進三種不同的電視機50臺,請你設計進貨方案.
若商場準備用9萬元同時購進三種不同的電視機50臺,請你設計進貨方案.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com