
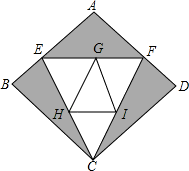
 種植成本降低了1成,使每平方米荷花和每平方米茉莉的種植總成本提高了8%.
種植成本降低了1成,使每平方米荷花和每平方米茉莉的種植總成本提高了8%.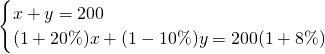

 x2+
x2+ ×8(8-x)×2]平方米.
×8(8-x)×2]平方米. x2-
x2- ×8(8-x)×2]×
×8(8-x)×2]× 平方米.
平方米. x2+
x2+ ×8(8-x)×2]×144+[82-
×8(8-x)×2]×144+[82- x2-
x2- ×8(8-x)×2]×
×8(8-x)×2]× ×72=7956
×72=7956 x2+
x2+ ×8(8-x)×2]平方米,再根據點G、H、I分別是EF、CE、CF的中點得到HI、GH、GI均為△CEF的中位線,然后表示出茉莉的種植面積,根據種植成本為7956元列出方程求得x的值即可求得AE的長.
×8(8-x)×2]平方米,再根據點G、H、I分別是EF、CE、CF的中點得到HI、GH、GI均為△CEF的中位線,然后表示出茉莉的種植面積,根據種植成本為7956元列出方程求得x的值即可求得AE的長.

 一諾書業暑假作業快樂假期云南美術出版社系列答案
一諾書業暑假作業快樂假期云南美術出版社系列答案科目:初中數學 來源: 題型:
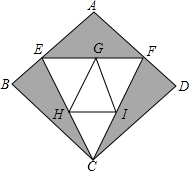 種植成本降低了1成,使每平方米荷花和每平方米茉莉的種植總成本提高了8%.
種植成本降低了1成,使每平方米荷花和每平方米茉莉的種植總成本提高了8%.查看答案和解析>>
科目:初中數學 來源:2013年貴州省黔西南州興義市豬場坪鄉中學中考數學模擬試卷(解析版) 題型:解答題
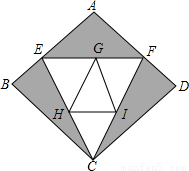
查看答案和解析>>
科目:初中數學 來源:2012年江蘇省蘇州市中考數學模擬試卷(五)(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com