
【題目】如圖,拋物線![]() 與直線
與直線![]() 分別相交于
分別相交于![]() ,
,![]() 兩點,且此拋物線與
兩點,且此拋物線與![]() 軸的一個交點為
軸的一個交點為![]() ,連接
,連接![]() ,
,![]() .已知
.已知![]() ,
,![]() .
.
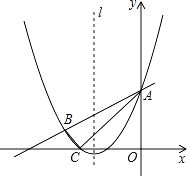
(1)求拋物線的解析式;
(2)在拋物線對稱軸![]() 上找一點
上找一點![]() ,使
,使![]() 的值最大,并求出這個最大值;
的值最大,并求出這個最大值;
(3)點![]() 為
為![]() 軸右側(cè)拋物線上一動點,連接
軸右側(cè)拋物線上一動點,連接![]() ,過點
,過點![]() 作
作![]() 交
交![]() 軸于點
軸于點![]() ,問:是否存在點
,問:是否存在點![]() 使得以
使得以![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 相似?若存在,請求出所有符合條件的點
相似?若存在,請求出所有符合條件的點![]() 的坐標(biāo);若不存在,請說明理由.
的坐標(biāo);若不存在,請說明理由.
【答案】(1)![]() ;(2)點M的坐標(biāo)為(
;(2)點M的坐標(biāo)為(![]() ,
,![]() )時,
)時,![]() 取最大值為
取最大值為![]() ;(3)存在點
;(3)存在點![]() .
.
【解析】
(1)根據(jù)待定系數(shù)法求解即可;
(2)根據(jù)三角形的三邊關(guān)系可知:當(dāng)點![]() 、
、![]() 、
、![]() 三點共線時,可使
三點共線時,可使![]() 的值最大,據(jù)此求解即可;
的值最大,據(jù)此求解即可;
(3)先求得![]() ,再過點
,再過點![]() 作
作![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() ,如圖,這樣就把以
,如圖,這樣就把以![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 相似問題轉(zhuǎn)化為以
相似問題轉(zhuǎn)化為以![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 相似的問題,再分當(dāng)
相似的問題,再分當(dāng)![]() 時與
時與![]() 時兩種情況,分別求解即可.
時兩種情況,分別求解即可.
解:(1)將![]() ,
,![]() 代入
代入![]() 得:
得:
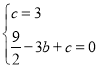 ,解得:
,解得:![]() ,
,
∴拋物線的解析式是![]() ;
;
(2)解方程組: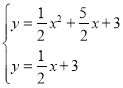 ,得
,得![]() ,
, ,
,
∵![]() ,∴
,∴![]()
當(dāng)點![]() 、
、![]() 、
、![]() 三點不共線時,根據(jù)三角形三邊關(guān)系得
三點不共線時,根據(jù)三角形三邊關(guān)系得![]() ,
,
當(dāng)點![]() 、
、![]() 、
、![]() 三點共線時,
三點共線時,![]() ,
,
∴當(dāng)點![]() 、
、![]() 、
、![]() 三點共線時,
三點共線時,![]() 取最大值,即為
取最大值,即為![]() 的長,
的長,
如圖,過點![]() 作BE⊥x軸于點
作BE⊥x軸于點![]() ,則在
,則在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,∴
,∴![]() 取最大值為
取最大值為![]() ;
;
易求得直線BC的解析式為:y=-x-3,拋物線的對稱軸是直線![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]() ,∴點M的坐標(biāo)為(
,∴點M的坐標(biāo)為(![]() ,
,![]() );
);
∴點M的坐標(biāo)為(![]() ,
,![]() )時,
)時,![]() 取最大值為
取最大值為![]() ;
;
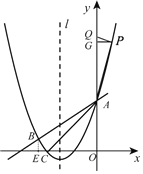
(3)存在點![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 為頂點的三角形與
為頂點的三角形與![]() 相似.
相似.
設(shè)點![]() 坐標(biāo)為
坐標(biāo)為![]() ,
,
在![]() 中,∵
中,∵![]() ,∴
,∴![]() ,
,
在![]() 中,∵
中,∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
過點![]() 作
作![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() ,如圖,
,如圖,
∵![]() ,
,![]() ,∴
,∴![]() ∽
∽![]() ,
,
∵![]() ,
,
∴①當(dāng)![]() 時,
時,![]() ∽
∽![]() ,
,
∴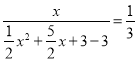 ,解得
,解得![]() ,
,![]() ,(舍去)
,(舍去)
∴點![]() 的縱坐標(biāo)為
的縱坐標(biāo)為![]() ,∴點
,∴點![]() 為
為![]() ;
;
②當(dāng)![]() 時,
時,![]() ∽
∽![]() ,
,
∴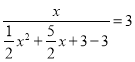 ,解得
,解得![]() (舍去),
(舍去),![]() (舍去),
(舍去),
∴此時無符合條件的點![]() ;
;
綜上所述,存在點![]() .
.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】材料閱讀:
類比是數(shù)學(xué)中常用的數(shù)學(xué)思想.比如,我們可以類比多位數(shù)的加、減、乘、除的豎式運算方法,得到多項式與多項式的加、減、乘、除的運算方法.

理解應(yīng)用:
(1)請仿照上面的豎式方法計算:![]() ;
;
(2)已知兩個多項式的和為![]() ,其中一個多項式為
,其中一個多項式為![]() .請用豎式的方法求出另一個多項式.
.請用豎式的方法求出另一個多項式.
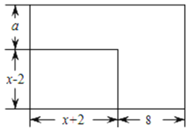
(3)已知一個長為![]() ,寬為
,寬為![]() 的矩形
的矩形![]() ,將它的長增加8.寬增加
,將它的長增加8.寬增加![]() 得到一個新矩形
得到一個新矩形![]() ,且矩形
,且矩形![]() 的周長是
的周長是![]() 周長的3倍(如圖).同時,矩形
周長的3倍(如圖).同時,矩形![]() 的面積和另一個一邊長為
的面積和另一個一邊長為![]() 的矩形
的矩形![]() 的面積相等,求
的面積相等,求![]() 的值和矩形
的值和矩形![]() 的另一邊長.
的另一邊長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,以AB為直徑的⊙O分別與BC,AC交于點D,E,過點D作DF⊥AC,垂足為點F.
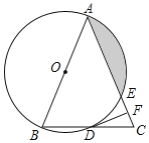
(1)求證:直線DF是⊙O的切線;
(2)求證:BC2=4CFAC;
(3)若⊙O的半徑為4,∠CDF=15°,求陰影部分的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在“停課不停學(xué)”期間,小明用電腦在線上課,圖1是他的電腦液晶顯示器的側(cè)面圖,顯示屏AB可以繞O點旋轉(zhuǎn)一定角度.研究表明:當(dāng)眼睛E與顯示屏頂端A在同一水平線上,且望向顯示器屏幕形成一個18°俯角(即望向屏幕中心P的的視線EP與水平線EA的夾角∠AEP)時,對保護(hù)眼睛比較好,而且顯示屏頂端A與底座C的連線AC與水平線CD垂直時(如圖2)時,觀看屏幕最舒適,此時測得∠BCD=30°,∠APE=90°,液晶顯示屏的寬AB為32cm.
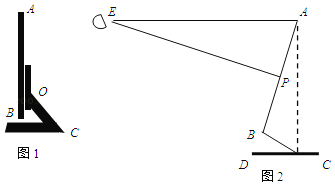
(1)求眼睛E與顯示屏頂端A的水平距離AE;(結(jié)果精確到1cm)
(2)求顯示屏頂端A與底座C的距離AC.(結(jié)果精確到1cm)(參考數(shù)據(jù):sin18°≈0.3,cos18°≈0.9,tan18°≈0.3,![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
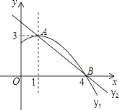
【題目】如圖是拋物線y1=ax2+bx+c(a≠0)圖象的一部分,拋物線的頂點坐標(biāo)A(1,3),與x軸的一個交點B(4,0),直線y2=mx+n(m≠0)與拋物線交于A,B兩點,下列結(jié)論: ①2a+b=0;②abc>0;③方程ax2+bx+c=3有兩個相等的實數(shù)根;④拋物線與x軸的另一個交點是(﹣1,0);⑤當(dāng)1<x<4時,有y2<y1 ,
其中正確的是________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩地相距![]() 一列快車和一列慢車都從甲地駛往乙地,慢車先行駛1小時后,快車才開始行駛.已知快車的速度是
一列快車和一列慢車都從甲地駛往乙地,慢車先行駛1小時后,快車才開始行駛.已知快車的速度是![]() 以快車開始行駛計時,設(shè)時間為
以快車開始行駛計時,設(shè)時間為![]() , 兩車之間的距離為
, 兩車之間的距離為![]() ,圖中的折線是
,圖中的折線是![]() 與
與![]() 的函數(shù)關(guān)系的部分圖象,根據(jù)圖象解決以下問題:
的函數(shù)關(guān)系的部分圖象,根據(jù)圖象解決以下問題:

(1)慢車的速度是_ _![]() ,點
,點![]() 的坐標(biāo)是_ _;
的坐標(biāo)是_ _;
(2)線段![]() 所表示的
所表示的![]() 與
與![]() 之間的函數(shù)關(guān)系式是_ ;
之間的函數(shù)關(guān)系式是_ ;
(3)試在圖中補(bǔ)全點![]() 以后的圖象.
以后的圖象.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知網(wǎng)格的小正方形的邊長均為1,格點三角形ABC如圖所示,請用沒有刻度的直尺畫出滿足條件的圖形
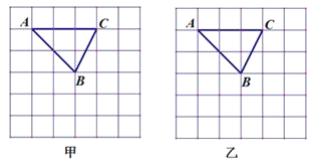
(1)在甲圖中,畫出△![]() ,且相似比為2:1,各頂點都在格點上.
,且相似比為2:1,各頂點都在格點上.
(2)在乙圖中,把線段AB三等分.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】《九章算術(shù)》作為古代中國乃至東方的第一部自成體系的數(shù)學(xué)專著,與古希臘的《幾何原本》并稱現(xiàn)代數(shù)學(xué)的兩大源泉.在《九章算術(shù)》中記載有一問題“今有圓材埋在壁中,不知大小.以鋸鋸之,深一寸,鋸道長一尺,問徑幾何?”小輝同學(xué)根據(jù)原文題意,畫出圓材截面圖如圖所示,已知:鋸口深為 1寸,鋸道AB=1尺(1尺=10寸),則該圓材的直徑為( )
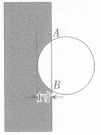
A.13B.24C.26D.28
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
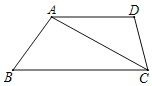
【題目】如圖,在四邊形ABCD中,AD∥BC.
(1)求作直線EF使得EF交AD于點E,交BC于點F且使得EA=EC,FA=FC(尺規(guī)作圖,保留作圖痕跡,不寫作法);
(2)連接AF、CE,判斷四邊形AFCE的形狀,并說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com