
【題目】我校八年級的體育老師為了了解本年級學生喜歡球類運動的情況,抽取了該年級部分學生對籃球、足球、排球、乒乓球的愛好情況進行了調查,并將調查結果繪制成如圖兩幅不完整的統計圖(說明:每位學生只選一種自己最喜歡的一種球類),請根據這兩幅圖形解答下列問題:
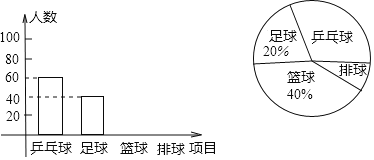
(1)在本次調查中,體育老師一共調查了多少名學生?
(2)將兩個不完整的統計圖補充完整;
(3)求出乒乓球在扇形中所占的圓心角的度數?
(4)已知該校有760名學生,請你根據調查結果估計愛好足球和排球的學生共計多少人?
【答案】(1)200人;(2)60人,30%, 10%,20人,80人,圖見解析;(3)108°;(4)228人.
【解析】
(1)讀圖可知喜歡足球的有40人,占20%,求出總人數;
(2)根據總人數求出喜歡乒乓球的人數所占的百分比,得出喜歡排球的人數和所占的百分比,再根據喜歡籃球的人數所占的百分比求出喜歡籃球的人數,從而補全統計圖;
(3)根據喜歡乒乓球的人數所占的百分比,即可得到乒乓球在扇形中所占的圓心角的度數;
(4)根據愛好足球和排球的學生所占的百分比,即可估計愛好足球和排球的學生總數.
解:(1)∵喜歡足球的有40人,占20%,
∴一共調查了:40÷20%=200(人),
(2)∵喜歡乒乓球人數為60人,
∴所占百分比為:![]() ×100%=30%,
×100%=30%,
∴喜歡排球的人數所占的百分比是1-20%-30%-40%=10%,
∴喜歡排球的人數為:200×10%=20(人),
∴喜歡籃球的人數為200×40%=80(人),
由以上信息補全條形統計圖得:
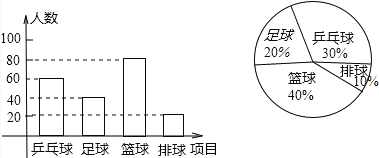
(3)乒乓球在扇形中所占的圓心角的度數為:30%×360°=108°;
(4)愛好足球和排球的學生共計:760×(20%+10%)=228(人).
故答案為:(1)200人;(2)60人,30%, 10%,20人,80人,圖見解析;(3)108°;(4)228人.


 輕巧奪冠周測月考直通中考系列答案
輕巧奪冠周測月考直通中考系列答案科目:初中數學 來源: 題型:
【題目】如圖,圓E是三角形ABC的外接圓, ∠BAC=45°,AO⊥BC于O,且BO=2,CO=3,分別以BC、AO所在直線建立x軸.
(1)求三角形ABC的外接圓直徑;
(2)求過ABC三點的拋物線的解析式;
(3)設P是(2)中拋物線上的一個動點,且三角形AOP為直角三角形,則這樣的點P有幾個?(只需寫出個數,無需解答過程).

查看答案和解析>>
科目:初中數學 來源: 題型:
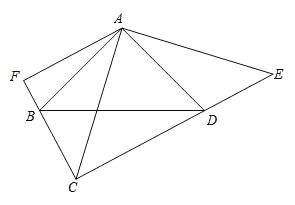
【題目】如圖, BAD CAE 90 , AB AD , AE AC , ABD ADB ACE AEC 45 ,AF CF ,垂足為 F .
(1)若 AC 10 ,求四邊形 ABCD 的面積;
(2)求證: CE 2 AF .
查看答案和解析>>
科目:初中數學 來源: 題型:
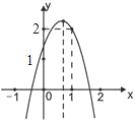
【題目】如圖,二次函數y=ax2+bx+c(a≠0)的圖象經過點(1,2)且與x軸交點的橫坐標分別為x1,x2,其中﹣1<x1<0.1<x2<2.下列結論:4a+2b+c<0;2a+b<0;b2+8a>4ac;
a<﹣1;其中結論正確的有( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
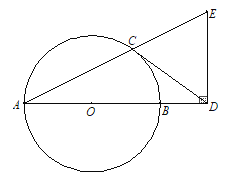
【題目】如圖,AB是⊙O的直徑,CD與⊙O相切于點C,與AB的延長線交于點D,DE⊥AD且與AC的延長線交于點E.
(1)求證:DC=DE;
(2)若tan∠CAB=![]() ,AB=3,求BD的長.
,AB=3,求BD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市為慶祝開業舉辦大酬賓抽獎活動,凡在開業當天進店購物的顧客,都能獲得一次抽獎的機會,抽獎規則如下:在一個不透明的盒子里裝有分別標有數字1、2、3、4的4個小球,它們的形狀、大小、質地完全相同,顧客先從盒子里隨機取出一個小球,記下小球上標有的數字,然后把小球放回盒子并攪拌均勻,再從盒子中隨機取出一個小球,記下小球上標有的數字,并計算兩次記下的數字之和,若兩次所得的數字之和為8,則可獲得50元代金券一張;若所得的數字之和為6,則可獲得30元代金券一張;若所得的數字之和為5,則可獲得15元代金券一張;其他情況都不中獎.
(1)請用列表或樹狀圖(樹狀圖也稱樹形圖)的方法(選其中一種即可),把抽獎一次可能出現的結果表示出來;
(2)假如你參加了該超市開業當天的一次抽獎活動,求能中獎的概率P.
查看答案和解析>>
科目:初中數學 來源: 題型:
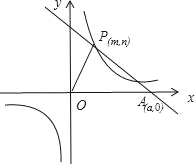
【題目】已知:O是坐標原點,P(m,n)(m>0)是函數y=![]() (k>0)上的點,過點P作直線PA⊥OP于P,直線PA與x軸的正半軸交于點A(a,0)(a>m).設△OPA的面積為s,且s=1+
(k>0)上的點,過點P作直線PA⊥OP于P,直線PA與x軸的正半軸交于點A(a,0)(a>m).設△OPA的面積為s,且s=1+![]() .
.
(1)當n=1時,求點A的坐標;
(2)若OP=AP,求k的值;
(3)設n是小于20的整數,且k≠![]() ,求OP2的最小值.
,求OP2的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△OAB是⊙O的內接三角形,∠AOB=120°,過O作OE⊥AB于點E,交⊙O于點C,延長OB至點D,使OB=BD,連CD.
(1)求證: CD是⊙O切線;
(2)若F為OE上一點,BF的延長線交⊙O于G,連OG,![]() ,CD=6
,CD=6![]() ,求S△GOB.
,求S△GOB.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,E是AB上一點,F是AD延長線上一點,且DF=BE.

(1)求證:CE=CF;
(2)若點G在AD上,且∠GCE=45°,則GE=BE+GD成立嗎?為什么?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com