Question

如圖，Rt△ABC中∠C=90°，∠A=30°在AC邊上取點O畫圓使⊙O經過A、B兩點，下列結論中：①；②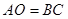；③以O為圓心，以OC為半徑的圓與AB相切；④延長BC交⊙O與D，則A、B、D是⊙O的三等分點．正確的序號是        ．

Answer 1

①③④

解析試題分析：連接OB，可得∠ABO=30°，則∠OBC=30°，根據直角三角形的性質得OC=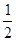OB=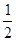OA，再根據三角函數cos∠O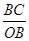BC=，則BC=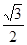OB，因為點O在∠ABC的角平分線上，所以點O到直線AB的距離等于OC的長，根據垂徑定理得直線AC是弦BD的垂直平分線，則點A、B、D將⊙O的三等分．
連接OB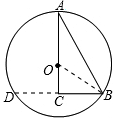

∴OA=OB，
∴∠A=∠ABO，
∵∠C=90°，∠A=30°，
∴∠ABC=60°，
∴∠OBC=30°，
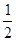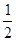∴OC=OB=OA，
即OA=2OC，
故①正確；
∵cos∠OBC=，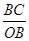
∴BC=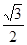OB，即BC=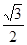OA
故②錯誤；
∵∠ABO=∠OBC=30°，
∴點O在∠ABC的角平分線上，
∴點O到直線AB的距離等于OC的長，
即以O為圓心，以OC為半徑的圓與AB相切；
故③正確；
延長BC交⊙O于D，
∵AC⊥BD，
∴AD=AB，
∴△ABD為等邊三角形，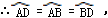

∴點A、B、D將⊙O的三等分．
故④正確．
故答案為①③④．
考點：直角三角形的性質，勾股定理，垂徑定理，角平分線的判定和性質，等邊三角形的判定和性質
點評：本題知識點多，綜合性強，是中考常見題，需要學生熟練掌握平面圖形的基本概念，難度較大.