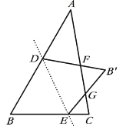
【題目】如圖，△ABC 中,∠B=60°，∠C=80°，點D,E分別在線段AB，BC 上， 將△BDE 沿直線DE翻折，使B落在B′ 處, B′ D, B′E分別交AC于F,G. 若∠ADF=70°，則∠CGE 的度數為______.
【答案】500
【解析】
連接BB'，由翻折變換的性質得：∠ABC=∠DB'E=60°，再根據三角形外角性質，即可得到∠ADF+∠CEG=60°+60°=120°，進而得出∠CEG=50°，再根據三角形內角和定理，即可得到△CEG中，∠CGE=180°-50°-80°=50°．
如圖，連接BB'，
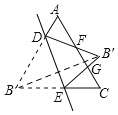
由翻折變換的性質得：∠ABC=∠DB'E=60°，
∵∠ADF是△BDB'的外角，∠CEG是△BEB'的外角，
∴∠ADF+∠CEG=60°+60°=120°，
又∵∠ADF=70°，
∴∠CEG=50°，
又∵∠C=80°，
∴△CEG中，∠CGE=180°-50°-80°=50°，
故答案為：50°．
科目：初中數學 來源： 題型：
【題目】已知反比例函數
（k為常數，k≠1）．
（Ⅰ）其圖象與正比例函數y=x的圖象的一個交點為P，若點P的縱坐標是2，求k的值；
（Ⅱ）若在其圖象的每一支上，y隨x的增大而減小，求k的取值范圍；
（Ⅲ）若其圖象的一支位于第二象限，在這一支上任取兩點A（x1，y1）、B（x2，y2），當y1＞y2時，試比較x1與x2的大小．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖是一根起點為1的數軸，現有同學將它彎折，彎折后虛線上第一行的數是1，第二行的數是13，第三行的數是43，…，依此規律，第五行的數是（ ）
A. 183 B. 157 C. 133 D. 91
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某物流公司承接A、B兩種貨物運輸業務，已知3月份A貨物運費單價為50元/噸，B貨物運費單價為30元/噸，共收取運費9500元；4月份由于工人工資上漲，運費單價上漲情況為：A貨物運費單價增加了40%，B貨物運費單價上漲到40元/噸；該物流公司4月承接的A種貨物和B種數量與3月份相同，4月份共收取運費13000元．試求該物流公司月運輸A、B兩種貨物各多少噸？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，填空:
(1)若∠4=∠3，則____∥_____，理由是______；
(2)若∠2=∠E，則____∥___，理由是____；
(3)若∠A=∠ABE=180°，則____∥___，理由是____；
(4)若∠2=∠____，則DA∥EB，理由是____；
(5)若∠DBC+∠_____=180°，則DB∥EC，理由是____；
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖①所示，已知，BC∥OA，∠B=∠A=100°，試解答下列問題：
（1）試說明：OB∥AC；
（2）如圖②，若點E．F在BC上，且∠FOC=∠AOC，OE平分∠BOF.試求∠EOC的度數；
（3）在（2）小題的條件下，若左右平行移動AC，如圖③，那么∠OCB：∠OFB的比值是否隨之發生變化？若變化，試說明理由；若不變，求出這個比值.
（4）在（3）小題的條件下，當∠OEB=∠OCA時，試求∠OCA的度數.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系 
中，已知點 
， 
．若平移點 
到點 
，使以點 
， ， ， 
為頂點的四邊形是菱形，則正確的平移方法是（ ）
A.向左平移1個單位，再向下平移1個單位
B.向左平移 
個單位，再向上平移1個單位
C.向右平移 
個單位，再向上平移1個單位
D.向右平移1個單位，再向上平移1個單位
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下列材料：通過小學的學習我們知道，分數可分為“真分數”和“假分數”，而假分數都可化為常分數，如： 
＝ 
＝2+ 
＝2 ．我們定義：在分式中，對于只含有一個字母的分式，當分子的次數大于或等于分母的次數時，我們稱之為“假分式”；當分子的次數小于分母的次數時，我們稱之為“真分式”．如 
，
這樣的分式就是假分式；再如：
，
這樣的分式就是真分式．類似的，假分式也可以化為帶分式（即：整式與真分式的和的形式）．如：
=1-
；
解決下列問題：
（1）分式 
是 分式（填“真分式”或“假分式”）；
（2）
將假分式化為帶分式；
（3）如果 x 為整數，分式 
的值為整數，求所有符合條件的 x 的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
