
【題目】如圖,一次函數y1=-![]() x+b的圖象與反比例函數y2=
x+b的圖象與反比例函數y2=![]() (x>0)的圖象交于A、B兩點,與x軸交于點C,且點A的坐標為(1,2),點B的橫坐標為3.
(x>0)的圖象交于A、B兩點,與x軸交于點C,且點A的坐標為(1,2),點B的橫坐標為3.
(1)在第一象限內,當x取何值時,y1>y2?(根據圖直接寫出結果)
(2)求反比例函數的解析式及△AOB的面積.

【答案】(1)1<x<3;(2)![]() ,面積為
,面積為![]() .
.
【解析】
(1)根據交點坐標,由函數圖象即可求解;
(2)運用待定系數法,求得一次函數和反比例函數的解析式,再根據解方程組求得C(0,4),最后根據S△AOB=S△AOC-S△BOC進行計算即可求解.
(1)根據圖象得:在第一象限內,當1<x<3時,y1>y2.
(2)把A(1,2)代入y2=![]() 中得k2=1×2=2,
中得k2=1×2=2,
∴反比例函數的解析式為y2=![]() ,
,
分別過點A、B作AE⊥x軸于E,BF⊥x軸于F,則AE=yA=2,
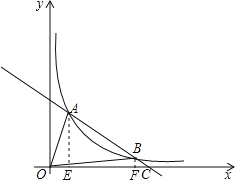
把xB=3代入y2=![]() 中,得yB=
中,得yB=![]() ,則BF=
,則BF=![]() ,
,
把A(1,2)代入y1=![]() x+b中,得:
x+b中,得:![]() +b=2,
+b=2,
∴b=![]() .
.
∴一次函數的解析式為y1=![]() x+
x+![]() ;
;
當yc=0時,![]() x+
x+![]() =0,得:x=4,則OC=4,
=0,得:x=4,則OC=4,
∴S△AOB=S△AOC-S△BOC=![]() OC(AEBF)=
OC(AEBF)= ![]() ×4(2
×4(2![]() )=
)=![]() .
.


科目:初中數學 來源: 題型:
【題目】某商場銷售一種西裝和領帶,西裝每套定價500元,領帶每條定價100元.元旦甲、乙兩商家促銷打折
甲商場:買一套西裝送一條領帶;
乙商場:西裝和領帶都按定價的![]() 付款.
付款.
現某客戶要購買西裝10套,領帶![]() 條
條![]() .
.
(1)若該客戶去甲商場購買,需付款多少元?(用含![]() 的代數式表示)若該客戶去乙商場購買,需付款多少元?(用含
的代數式表示)若該客戶去乙商場購買,需付款多少元?(用含![]() 的代數式表示)
的代數式表示)
(2)若![]() 等于20,通過計算說明此時去哪家商場買更合算?
等于20,通過計算說明此時去哪家商場買更合算?
(3)當![]() 時,你能給出一種更為省錢的購買方案嗎?
時,你能給出一種更為省錢的購買方案嗎?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形紙片ABCD中,對角線AC、BD交于點O,折疊正方形紙片ABCD,使AD落在BD上,點A恰好與BD上的點F重合.展開后,折痕DE分別交AB、AC于點E、G.連接GF.下列結論:①∠AGD=112.5°;②tan∠AED=2;③S△AGD=S△OGD;④四邊形AEFG是菱形;⑤BE=2OG.
其中正確結論的序號是( )

A. ①②③④⑤ B. ①②③④ C. ①③④⑤ D. ①④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為實施鄉村振興戰略,解決某山區老百姓出行難的問題,當地政府決定修建一條高速公路.其中一段長為146米的山體隧道貫穿工程由甲乙兩個工程隊負責施工.甲工程隊獨立工作2天后,乙工程隊加入,兩工程隊又聯合工作了1天,這3天共掘進26米.已知甲工程隊每天比乙工程隊多掘進2米,按此速度完成這項隧道貫穿工程,甲乙兩個工程隊還需聯合工作多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線l經過⊙O的圓心O,且與⊙O交于A、B兩點,點C在⊙O上,且∠AOC=30°,點P是直線l上的一個動點(與圓心O不重合),直線CP與⊙O相交于另一點Q,如果QP=QO,則∠OCP= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,線段CD在線段AB上,且CD=2,若線段AB的長度是一個正整數,則圖中以A,B,C,D這四點中任意兩點為端點的所有線段長度之和可能是( )![]()
A. 29
B. 28
C. 30
D. 31
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小方家住戶型呈長方形,平面圖如下(單位:米),現準備鋪設地面,三間臥室鋪設木地板,其它區城鋪設地磚.

(1)求a的值.
(2)鋪設地面需要木地板和地磚各多少平方米(用含![]() 的代數式表示)?
的代數式表示)?
(3)按市場價格,木地板單價為300元/平方米,地磚單價為100元/平方米,裝修公司有![]() 兩種活動方案,如表:
兩種活動方案,如表:
活動方案 | 木地板價格 | 地磚價格 | 總安裝費 |
A | 8折 | 8.5折 | 2000元 |
B | 9折 | 8.5折 | 免收 |
已知臥室2的面積是21平方米,則小方家應選擇哪種活動,使鋪設地面的總費用(包括材料費及安裝費)更低?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】目前節能燈在城市已基本普及,某商場計劃購進甲、乙兩種節能燈共1200只,這兩種節能燈的進價、售價如下表:
| 進價 | 售價 |
甲型 | 25 | 30 |
乙型 | 45 | 60 |
![]() 如何進貨,進貨款恰好為46000元?
如何進貨,進貨款恰好為46000元?
![]() 為確保乙型節能燈順利暢銷,在
為確保乙型節能燈順利暢銷,在![]() 的條件下,商家決定對乙型節能燈進行打折出售,且全部售完后,乙型節能燈的利潤率為
的條件下,商家決定對乙型節能燈進行打折出售,且全部售完后,乙型節能燈的利潤率為![]() ,請問乙型節能燈需打幾折?
,請問乙型節能燈需打幾折?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中央電視臺的“中國詩詞大賽”節目文化品位高,內容豐富,某校初二年級模擬開展“中國詩詞大賽”比賽,對全年級同學成績進行統計后分為“優秀”、“良好”、“一般”、“較差”四個等級,并根據成績繪制成如下兩幅不完整的統計圖,請結合統計圖中的信息,回答下列問題:

(1)扇形統計圖中“優秀”所對應的扇形的圓心角為 度,并將條形統計圖補充完整.
(2)此次比賽有四名同學活動滿分,分別是甲、乙、丙、丁,現從這四名同學中挑選兩名同學參加學校舉行的“中國詩詞大賽”比賽,請用列表法或畫樹狀圖法,求出選中的兩名同學恰好是甲、丁的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com