
【題目】如圖,在直角坐標系中,拋物線y=a(x-![]() )2+
)2+![]() 與⊙M交于A,B,C,D四點,點A,B在x軸上,點C坐標為(0,-2).
與⊙M交于A,B,C,D四點,點A,B在x軸上,點C坐標為(0,-2).
(1)求a值及A,B兩點坐標;
(2)點P(m,n)是拋物線上的動點,當∠CPD為銳角時,請求出m的取值范圍;
(3)點E是拋物線的頂點,⊙M沿CD所在直線平移,點C,D的對應點分別為點C′,D′,順次連接A,C′,D′,E四點,四邊形AC′D′E(只要考慮凸四邊形)的周長是否存在最小值?若存在,請求出此時圓心M′的坐標;若不存在,請說明理由.
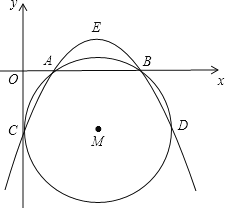
【答案】(1)A(1,0),B(4,0).(2)m<0或1<m<4或m>5.(3)存在.M′(![]() ,-2)
,-2)
【解析】
(1)把點C坐標代入拋物線解析式即可求出a,令y=0可得拋物線與x軸的交點坐標.
(2)根據題意可知,當點P在圓外部的拋物線上運動時,∠CPD為銳角,由此即可解決問題.
(3)存在.如圖2中,將線段C'A平移至D'F,當點D'與點H重合時,四邊形AC'D'E的周長最小,求出點H坐標即可解決問題.
解:(1)∵拋物線y=a(x-![]() )2+
)2+![]() 經過點C(0,-2),
經過點C(0,-2),
∴-2=a(0-![]() )2+
)2+![]() ,
,
∴a=-![]() ,
,
∴y=-![]() (x-
(x-![]() )2+
)2+![]() ,
,
當y=0時,-![]() (x-
(x-![]() )2+
)2+![]() =0,
=0,
∴x1=4,x2=1,
∵A、B在x軸上,
∴A(1,0),B(4,0).
(2)由(1)可知拋物線解析式為y=-![]() (x-
(x-![]() )2+
)2+![]() ,
,
∴C、D關于對稱軸x=![]() 對稱,
對稱,
∵C(0,-2),
∴D(5,-2),
如圖1中,連接AD、AC、CD,則CD=5,
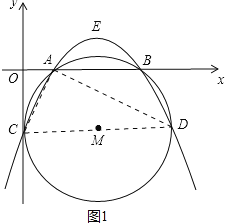
∵A(1,0),C(0,-2),D(5,-2),
∴AC=![]() ,AD=2
,AD=2![]() ,
,
∴AC2+AD2=CD2,
∴∠CAD=90°,
∴CD為⊙M的直徑,
∴當點P在圓外部的拋物線上運動時,∠CPD為銳角,
∴m<0或1<m<4或m>5.
(3)存在.如圖2中,將線段C′A平移至D′F,則AF=C′D′=CD=5,
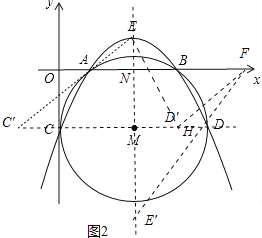
∵A(1,0),
∴F(6,0),
作點E關于直線CD的對稱點E′,
連接EE′正好經過點M,交x軸于點N,
∵拋物線頂點(![]() ,
,![]() ),直線CD為y=-2,
),直線CD為y=-2,
∴E′(![]() ,-
,-![]() ),
),
連接E′F交直線CD于H,
∵AE,C′D′是定值,
∴AC′+ED′最小時,四邊形AC′D′E的周長最小,
∵AC′+D′E=FD′+D′E=FD′+E′D′≥E′F,
則當點D′與點H重合時,四邊形AC′D′E的周長最小,
設直線E′F的解析式為y=kx+b,
∵E′(![]() ,-
,-![]() ),F(6,0),
),F(6,0),
∴可得y=![]() x-
x-![]() ,
,
當y=-2時,x=![]() ,
,
∴H(![]() ,-2),∵M(
,-2),∵M(![]() ,-2),
,-2),
∴DD′=5-![]() =
=![]() ,
,
∵![]() -
-![]() =
=![]() ,
,
∴M′(![]() ,-2)
,-2)


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,我們定義直線![]() 為拋物線
為拋物線![]() 、b、c為常數,
、b、c為常數,![]() 的“夢想直線”;有一個頂點在拋物線上,另有一個頂點在y軸上的三角形為其“夢想三角形”.
的“夢想直線”;有一個頂點在拋物線上,另有一個頂點在y軸上的三角形為其“夢想三角形”.

已知拋物線![]() 與其“夢想直線”交于A、B兩點
與其“夢想直線”交于A、B兩點![]() 點A在點B的左側
點A在點B的左側![]() ,與x軸負半軸交于點C.
,與x軸負半軸交于點C.
![]() 填空:該拋物線的“夢想直線”的解析式為______,點A的坐標為______,點B的坐標為______;
填空:該拋物線的“夢想直線”的解析式為______,點A的坐標為______,點B的坐標為______;
![]() 如圖,點M為線段CB上一動點,將
如圖,點M為線段CB上一動點,將![]() 以AM所在直線為對稱軸翻折,點C的對稱點為N,若
以AM所在直線為對稱軸翻折,點C的對稱點為N,若![]() 為該拋物線的“夢想三角形”,求點N的坐標;
為該拋物線的“夢想三角形”,求點N的坐標;
![]() 當點E在拋物線的對稱軸上運動時,在該拋物線的“夢想直線”上,是否存在點F,使得以點A、C、E、F為頂點的四邊形為平行四邊形?若存在,請直接寫出點E、F的坐標;若不存在,請說明理由.
當點E在拋物線的對稱軸上運動時,在該拋物線的“夢想直線”上,是否存在點F,使得以點A、C、E、F為頂點的四邊形為平行四邊形?若存在,請直接寫出點E、F的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲乙兩車從A地駛向B地,甲車比乙車早出發2h,并且甲車在途中休息了0.5h,甲、乙兩車離A地的距離y(km)與甲車行駛時間x(h)之間的函數圖象如圖所示.根據圖象提供的信息,下列說法:
①乙車速度比甲車慢;②a=40;③乙車比甲車早1.75小時到達B地.
其中正確的有( )
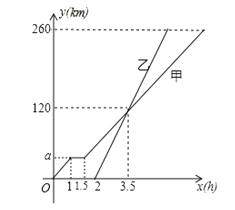
A.0個B.2個C.1個D.3個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】分別以□ABCD(∠CDA≠90°)的三邊AB,CD,DA為斜邊作等腰直角三角形,△ABE,△CDG,△ADF.
(1)如圖1,當三個等腰直角三角形都在該平行四邊形外部時,連接GF,EF.請判斷GF與EF的關系(只寫結論,不需證明);
(2)如圖2,當三個等腰直角三角形都在該平行四邊形內部時,連接GF,EF,(1)中結論還成立嗎?若成立,給出證明;若不成立,說明理由.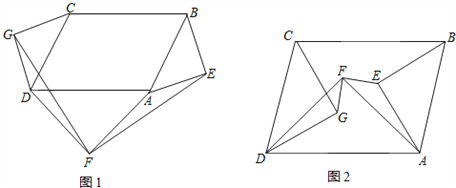
查看答案和解析>>
科目:初中數學 來源: 題型:
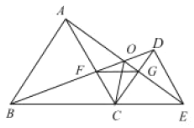
【題目】如圖,已知![]() 和
和![]() 均是等邊三角形,點
均是等邊三角形,點![]() 在同一條直線上,
在同一條直線上,![]() 與
與![]() 交于點
交于點![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,連接
,連接![]() ,則下列結論:①
,則下列結論:①![]() ;②
;②![]() ;③
;③![]() ﹔④
﹔④![]() ,其中正確結論有_________個.
,其中正確結論有_________個.
查看答案和解析>>
科目:初中數學 來源: 題型:
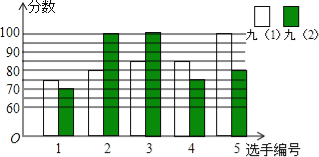
【題目】某中學開展“唱紅歌”比賽活動,九年級(1)、(2)班根據初賽成績,各選出5名選手參加復賽,兩個班各選出的5名選手的復賽成績(滿分為100分)如圖所示.
(1)根據圖示填寫下表;
班級 | 平均數(分) | 中位數(分) | 眾數(分) |
九(1) | 85 | 85 | |
九(2) | 80 |
(2)結合兩班復賽成績的平均數和中位數,分析哪個班級的復賽成績較好;
(3)計算兩班復賽成績的方差.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一塊長方形鏡面玻璃的四周鑲上與它的周長相等的邊框,制成一面鏡子,鏡子的長與寬的比是2:1,設制作這面鏡子的寬度是x米,總費用是y元,則y=240x2+180x+60.(注:總費用=鏡面玻璃的費用+邊框的費用+加工費).
(1)這塊鏡面玻璃的價格是每平方米 元,加工費 元;
(2)如果制作這面鏡子共花了210元,求這面鏡子的長和寬.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐角系中,點![]() 是原點,點
是原點,點![]() 、
、![]() 在坐標軸上,連接
在坐標軸上,連接![]() ,
,![]() ,點
,點![]() 在
在![]() 軸上,且點
軸上,且點![]() 是線段
是線段![]() 的垂直平分線上一點.
的垂直平分線上一點.
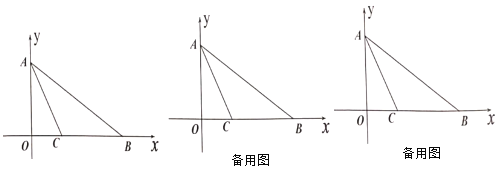
(1)求點![]() 的坐標;
的坐標;
(2)點![]() 從點
從點![]() 出發以每秒2個單位長度的速度向終點
出發以每秒2個單位長度的速度向終點![]() 運動(點
運動(點![]() 不與點
不與點![]() 重合),連接
重合),連接![]() 、
、![]() ,若點
,若點![]() 的運動時間為
的運動時間為![]() 秒,
秒,![]() 的面積為
的面積為![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ;
;
(3)在(2)的條件下,過點![]() 作
作![]() 垂直
垂直![]() 軸,交
軸,交![]() 于
于![]() ,若
,若![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com