
如圖1,△ABC是等腰直角三角形,四邊形ADEF是正方形,D、F分別在AB、AC邊上,此時BD=CF,BD⊥CF成立。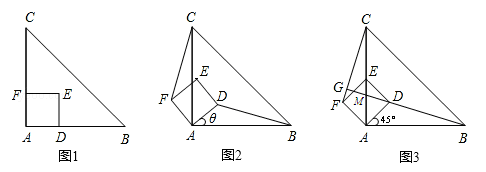
(1)當正方形ADEF繞點A逆時針旋轉θ(0°<θ<90°)時,如圖2,BD=CF成立嗎?若成立,請證明;若不成立,請說明理由。
(2)當正方形ADEF繞點A逆時針旋轉45°時,如圖3,延長BD交CF于點G。
求證:BD⊥CF。
(3)在(2)小題的條件下, AC與BG的交點為M, 當AB=4,AD= 時,求線段CM的長。
時,求線段CM的長。
解:(1)BD=CF成立。理由如下:
∵△ABC是等腰直角三角形,四邊形ADEF是正方形,
∴AB=AC,AD=AF,∠BAC=∠DAF=90°。
∵∠BAD=∠BAC﹣∠DAC,∠CAF=∠DAF﹣∠DAC,∴∠BAD=∠CAF。
在△BAD和△CAF中,∵AB=AC,∠BAD=∠CAF,
∴△BAD≌△CAF(SAS)。∴BD=CF。
(2)證明:∵△BAD≌△CAF(已證),∴∠ABM=∠GCM。
又∵∠BMA=∠CMG,∴△BMA∽△CMG。
∴∠BGC=∠BAC=90°。∴BD⊥CF。
(3)過點F作FN⊥AC于點N。
∵在正方形ADEF中,AD=DE= ,
,
∴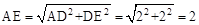 。
。
∴AN=FN= AE=1。
AE=1。
∵在等腰直角△ABC 中,AB=4,
∴CN=AC﹣AN=3, 。
。
∴在Rt△FCN中, ,
,
在Rt△ABM中, 。
。
∴AM= 。
。
∴CM=AC-AM=4-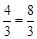 。
。
解析試題分析:(1)△ABC是等腰直角三角形,四邊形ADEF是正方形,易證得△BAD≌△CAF,根據全等三角形的對應邊相等,即可證得BD=CF。
(2)由△BAD≌△CAF,可得∠ABM=∠GCM,又由對頂角相等,易證得△BMA∽△CMG,根據相似三角形的對應角相等,可得BGC=∠BAC=90°,即可證得BD⊥CF。
(3)首先過點F作FN⊥AC于點N,利用勾股定理即可求得AE,BC的長,繼而求得AN,CN的長,又由等角的三角函數值相等,可求得AM= 。從而可求得線段CM的長。
。從而可求得線段CM的長。


科目:初中數學 來源: 題型:解答題
如圖,已知△ABC是邊長為6cm的等邊三角形,動點P,Q同時從A、B兩點出發,分別沿AB,BC方向勻速運動,其中點P運動的速度是1cm/s,點Q運動的速度是2cm/s,當點Q到達點C時,P、Q兩點都停止運動,設運動時間為t(s),
解答下列問題:
(1)當 為何值時,△BPQ為直角三角形;
為何值時,△BPQ為直角三角形;
(2)設△BPQ的面積為S(cm2),求S與 的函數關系式;
的函數關系式;
(3)作QR∥BA交AC于點R,連結PR,當 為何值時,△APR∽△PRQ ?
為何值時,△APR∽△PRQ ?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,∴P是菱形ABCD對角線AC上的一點,連接DP并延長DP交邊AB于點E,連接BP并延長BP交邊AD于點F,交CD的延長線于點G.
(1)求證:△APB≌△APD;
(2)已知DF:FA=1:2,設線段DP的長為x,線段PF的長為y.
①求y與x的函數關系式;
②當x=6時,求線段FG的長.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
在矩形ABCD中,點P是邊AD上的動點,連接BP,線段BP的垂直平分線交邊BC于點Q,垂足為點M,連接QP(如圖).已知AD=13,AB=5,設AP=x,BQ=y.
(1)求y關于x的函數解析式,并寫出x的取值范圍;
(2)當以AP長為半徑的⊙P和以QC長為半徑的⊙Q外切時,求x的值;
(3)點E在邊CD上,過點E作直線QP的垂線,垂足為F,如果EF=EC=4,求x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,矩形ABCD中,AB=12cm,AD=16cm,動點E、F分別從A點、C點同時出發,均以2cm/s的速度分別沿AD向D點和沿CB向B點運動。
(1)經過幾秒首次可使EF⊥AC?
(2)若EF⊥AC,在線段AC上,是否存在一點P,使 ?若存在,請說明P點的位置,并予以證明;若不存在,請說明理由。
?若存在,請說明P點的位置,并予以證明;若不存在,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,在矩形ABCD中,點P在邊CD上,且與C、D不重合,過點A作AP的垂線與CB的延長線相交于點Q,連接PQ,M為PQ中點.
(1)求證:△ADP∽△ABQ;
(2)若AD=10,AB=20,點P在邊CD上運動,設DP=x,BM2=y,求y與x的函數關系式,并求線段BM的最小值;
(3)若AD=10,AB=a,DP=8,隨著a的大小的變化,點M的位置也在變化.當點M落在矩形ABCD外部時,求a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖所示,在直角梯形ABCD中,AB為垂直于底邊的腰,AD=1,BC=2,AB=3,點E為CD上異于C,D的一個動點,過點E作AB的垂線,垂足為F,△ADE,△AEB,△BCE的面積分別為S1,S2,S3.
(1)設AF=x,試用x表示S1與S3的乘積S1S3,并求S1S3的最大值;
(2)設 =t,試用t表示EF的長;
=t,試用t表示EF的長;
(3)在(2)的條件下,當t為何值時,S22=4S1S3.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com