
(9分)如圖所示,在邊長為1的正方形ABCD中,一直角三角尺PQR的直角頂點P在對角線AC上移動,直角邊PQ經過點D,另一直角邊與射線BC交于點E.
⑴試判斷PE與PD的大小關系,并證明你的結論;
⑵連 接PB,試證明:△PBE為等腰三角形;
接PB,試證明:△PBE為等腰三角形;
⑶設AP=x,△PBE的面積為y,
①求出y關于x 函數關系式;
②當點P落在AC的何處時,△PBE的面積最大,此時最大值是多少?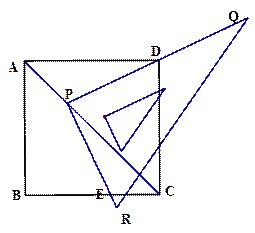
證明:(1) 過點P作GF∥AB,分別交AD、BC于G、F. 如圖所示.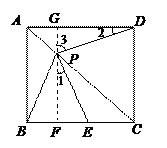
∵ 四邊形ABCD是正方形,
∴ 四邊形ABFG和四邊形GFCD都是矩形,
△AGP和△PFC都是等腰直角三角形………1分
∴ GD=FC=FP,GP=AG=BF,∠PGD=∠PFE=90°
又∵∠1+∠3=∠2+∠3=90°∴∠1=∠2………2 分
分
又PF=GD,∠PFE =∠PGD=90°
∴ Rt△EFP≌Rt△PGD(ASA). 
∴ PE=PD………3分
(2)∵AD=AB ∠PAB =∠PAD=45° AP=AP
=∠PAD=45° AP=AP
∴△APB≌△APD (SAS)………4 分
分
∴PB=PD
∴PE=PB
∴△PBE為等腰三角形 ………6分
(3)①∵AP=x
∴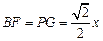 ,
,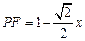 ………7分
………7分
∴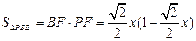
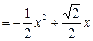 .
.
即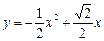 (
(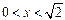 )………8分
)………8分
②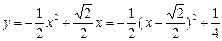 .
.
∵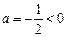 ,
,
∴當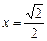 時,
時,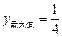 ………9分
………9分
解析


 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:初中數學 來源: 題型:
(本小題滿分12分)如圖所示,在梯形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 為直徑的
為直徑的![]() 與
與![]() 相切于
相切于![]() .已知
.已知![]() ,邊
,邊![]() 比
比![]() 大6.
大6.

(1)求邊 、
、 的長.
的長.
(2)在直徑 上是否存在一動點
上是否存在一動點 ,使以
,使以 、
、 、
、 為頂點的三角形與
為頂點的三角形與 相似?若存在,求出
相似?若存在,求出 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
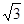 ,矩形ABOC繞點O按順時針方向旋轉60°后得矩形EFOD. 點A的對應點為點E,點B的對應點為F,點C的對應點為點D. 拋物線
,矩形ABOC繞點O按順時針方向旋轉60°后得矩形EFOD. 點A的對應點為點E,點B的對應點為F,點C的對應點為點D. 拋物線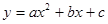 過點A、E、D.
過點A、E、D.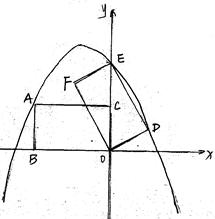
查看答案和解析>>
科目:初中數學 來源: 題型:
 中,
中, ,
, ,以
,以 為直徑的
為直徑的 與
與 相切于
相切于 .已知
.已知 ,邊
,邊 比
比 大6.
大6.
 、
、 的長.
的長. 上是否存在一動點
上是否存在一動點 ,使以
,使以 、
、 、
、 為頂點的三角形與
為頂點的三角形與 相似?若存在,求出
相似?若存在,求出 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.查看答案和解析>>
科目:初中數學 來源:2011年浙江省杭州市蕭山區中考數學模擬試卷 題型:解答題
(11·貴港)(本題滿分11分)
如圖所示,在以O為圓心的兩個同心圓中,小圓的半徑為1,AB與小圓相切于點A,與大圓相交于點B,大圓的弦BC⊥AB于點B,過點C作大圓的切線CD交AB的延長線于點D,連接OC交小圓于點E,連接BE、BO.
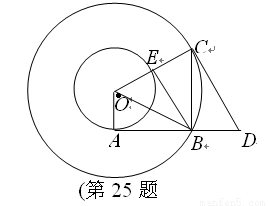
(1)求證:△AOB∽△BDC;
(2)設大圓的半徑為x,CD的長為y:
① 求y與x之間的函數關系式;
② 當BE與小圓相切時,求x的值.
查看答案和解析>>
科目:初中數學 來源:2010年安徽省蕪湖市畢業學業考試模擬試卷數學卷 題型:解答題
(本小題滿分12分)如圖所示,在梯形 中,
中, ,
,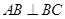 ,以
,以 為直徑的
為直徑的 與
與 相切于
相切于 .已知
.已知 ,邊
,邊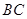 比
比 大6.
大6.

(1)求邊 、
、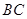 的長.
的長.
(2)在直徑 上是否存在一動點
上是否存在一動點 ,使以
,使以 、
、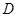 、
、 為頂點的三角形與
為頂點的三角形與 相似?若存在,求出
相似?若存在,求出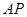 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com