
如圖,直線y=- x+6分別與x軸、y軸交于A、B兩點;直線y=
x+6分別與x軸、y軸交于A、B兩點;直線y= x與AB交于點C,與過點A且平行于y軸的直線交于點D.點E從點A出發,以每秒1個單位的速度沿
x與AB交于點C,與過點A且平行于y軸的直線交于點D.點E從點A出發,以每秒1個單位的速度沿 軸向左運動.過點E作x軸的垂線,分別交直線AB、OD于P、Q兩點,以PQ為邊向右作正方形PQMN,設正方形PQMN與△ACD重疊部分(陰影部分)的面積為S(平方單位),點E的運動時間為t(秒).
軸向左運動.過點E作x軸的垂線,分別交直線AB、OD于P、Q兩點,以PQ為邊向右作正方形PQMN,設正方形PQMN與△ACD重疊部分(陰影部分)的面積為S(平方單位),點E的運動時間為t(秒).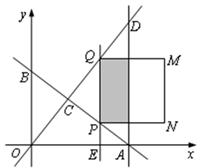
(1)求點C的坐標;
(2)當0<t<5時,求S與t之間的函數關系式,并求S的最大值;
(3)當t>0時,直接寫出點(4,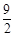 )在正方形PQMN內部時t的取值范圍.
)在正方形PQMN內部時t的取值范圍.
(1)(3,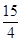 );(2)當0<t≤
);(2)當0<t≤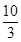 時,S=-2(t-
時,S=-2(t-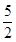 )2+
)2+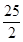 ,當
,當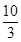 ≤t<5時,S=4(t-5)2,
≤t<5時,S=4(t-5)2,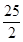 ;(3)
;(3)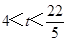 .
.
解析試題分析:(1)利用已知函數解析式,求兩直線的交點,得點C的坐標即可;
(2)根據幾何關系把s用t表示,注意當MN在AD上時,這一特殊情況,進而分類討論得出;
(3)利用(2)中所求,結合二次函數最值求法求出即可.
試題解析:(1)由題意,得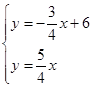 ,解得:
,解得: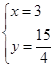 ,
,
∴C(3,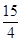 );
);
(2)∵直線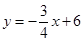 分別與x軸、y軸交于A、B兩點,
分別與x軸、y軸交于A、B兩點,
∴y=0時,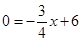 ,解得;x=8,
,解得;x=8,
∴A點坐標為;(8,0),
根據題意,得AE=t,OE=8-t.
∴點Q的縱坐標為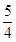 (8-t),點P的縱坐標為-
(8-t),點P的縱坐標為-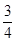 (8-t)+6=
(8-t)+6=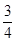 t,
t,
∴PQ=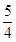 (8-t)-
(8-t)-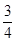 t=10-2t.
t=10-2t.
當MN在AD上時,10-2t=t,
∴t=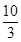 .
.
當0<t≤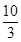 時,S=t(10-2t),即S=-2t2+10t.
時,S=t(10-2t),即S=-2t2+10t.
當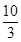 <t<5時,S=(10-2t)2,即S=4t2-40t+100;
<t<5時,S=(10-2t)2,即S=4t2-40t+100;
當0<t≤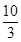 時,S=-2(t-
時,S=-2(t-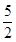 )2+
)2+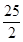 ,
,
∴t=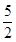 時,S最大值=
時,S最大值=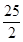 .
.
當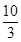 ≤t<5時,S=4(t-5)2,
≤t<5時,S=4(t-5)2,
∵t<5時,S隨t的增大而減小,
∴t=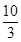 時,S最大值=
時,S最大值=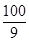 .
.
∵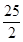 >
>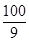 ,
,
∴S的最大值為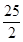 .
.
(3)點(4,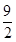 )在正方形PQMN內部時t的取值范圍是
)在正方形PQMN內部時t的取值范圍是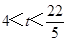 .
.
考點: 一次函數綜合題.


 藍天教育暑假優化學習系列答案
藍天教育暑假優化學習系列答案科目:初中數學 來源: 題型:解答題
為了節約資源,科學指導居民改善居住條件,小王向房管部門提出了一個購買商品房的政策性方案.
| 人均住房面積(平方米) | 單價(萬元/平方米) |
| 不超過30(平方米) | 0.3 |
| 超過30平方米不超過m(平方米)部分(45≤m≤60) | 0.5 |
| 超過m平方米部分 | 0.7 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,直線l與坐標軸分別交于A、B兩點,∠BAO=45°,點A坐標為(8,0).動點P從點O出發,沿折線段OBA運動,到點A停止;同時動點Q也從點O出發,沿線段OA運動,到點A停止;它們的運動速度均為每秒1個單位長度.
(1)求直線AB的函數關系式;
(2)若點A、B、O與平面內點E組成的圖形是平行四邊形,請直接寫出點E的坐標;
(3)在運動過程中,當P、Q的距離為2時,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,四邊形ABCD是平行四邊形,點A(1,0),B(3,1),C(3,3).反比例函數y= (x>0)的函數圖象經過點D,點P是一次函數y=kx+3-3k(k≠0)的圖象與該反比例函數圖象的一個公共點.
(x>0)的函數圖象經過點D,點P是一次函數y=kx+3-3k(k≠0)的圖象與該反比例函數圖象的一個公共點.
(1)求反比例函數的解析式;
(2)通過計算,說明一次函數y=kx+3-3k(k≠0)的圖象一定過點C;
(3)對于一次函數y=kx+3-3k(k≠0),當y隨x的增大而增大時,確定點P的橫坐標的取值范圍(不必寫出過程).
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
為鼓勵居民節約用水,某市決定對居民用水收費實行“階梯價”,即當每月用水量不超過15噸時(包括15噸),采用基本價收費;當每月用水量超過15噸時,超過部分每噸采用市場價收費,小蘭家4、5月份的用水量及收費情況如下表:
| 月份 | 用水量(噸) | 水費(元) |
| 4 | 22 | 51 |
| 5 | 20 | 45 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,在直角坐標系xOy中,直線 與雙曲線
與雙曲線 相交于
相交于 、B
、B 兩點,矩形
兩點,矩形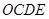 的邊
的邊 恰好被點
恰好被點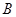 平分,邊
平分,邊 交雙曲線于
交雙曲線于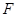 點,四邊形
點,四邊形 的面積為2.
的面積為2.
(1)求n的值;
(2)求不等式 的解集
的解集
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
四川省第十二屆運動會將于2014年8月18日在我市隆重開幕,根據大會組委會安排,某校接受了開幕式大型團體操表演任務.為此,學校需要采購一批演出服裝,A、B兩家制衣公司都愿成為這批服裝的供應商.經了解:兩家公司生產的這款演出服裝的質量和單價都相同,即男裝每套120元,女裝每套100元.經洽談協商:A公司給出的優惠條件是,全部服裝按單價打七折,但校方需承擔2200元的運費;B公司的優惠條件是男女裝均按每套100元打八折,公司承擔運費.另外根據大會組委會要求,參加演出的女生人數應是男生人數的2倍少100人,如果設參加演出的男生有x人.
(1)分別寫出學校購買A、B兩公司服裝所付的總費用y1(元)和y2(元)與參演男生人數x之間的函數關系式;
(2)問:該學校購買哪家制衣公司的服裝比較合算?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
小明從家騎自行車出發,沿一條直路到相距2400m的郵局辦事,小明出發的同時,他的爸爸以96m/min速度從郵局同一條道路步行回家,小明在郵局停留2min后沿原路以原速返回,設他們出發后經過t min時,小明與家之間的距離為s1 m,小明爸爸與家之間的距離為s2m,圖中折線OABD、線段EF分別表示s1、s2與t之間的函數關系的圖象.
(1)求s2與t之間的函數關系式;
(2)小明從家出發,經過多長時間在返回途中追上爸爸?這時他們距離家還有多遠?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com