日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 初中數學 > 題目詳情
已知四條線段成比例線段 , 其中三條線段長分別為4cm , 5cm和10cm , 那么第四條線段的長可能是 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （   ）

<

　　A.7.5cm    B.8.5cm    C.10.5cm    D.12.5cm

答案：D
提示：

設第四條線段的長x,列出成比例線段的比例式4：5=10：x。


練習冊系列答案
相關習題

科目：初中數學 來源： 題型：閱讀理解

請閱讀下面材料，并回答所提出的問題．
三角形內角平分線性質定理：三角形的內角平分線分對邊所得的兩條線段和這個角的兩邊對應成比例．
已知：如圖，△ABC中，AD是角平分線．
求證：
BD
DC
=
AB
AC

分析：要證
BD
DC
=
AB
AC
，一般只要證BD、DC與AB、AC或BD、AB與DC、AC所在三角形相似．現在B、D、C在一直線上，△ABD與△ADC不相似，需要考慮用別的方法換比．在比例式
BD
DC
=
AB
AC
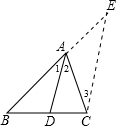中，AC恰是BD、DC、AB的第四比例項，所以考慮過C作C精英家教網E∥AD，交BA的延長線于E，從而得到BD、DC、AB的第四比例項AE，這樣，證明
BD
DC
=
AB
AC
就可以轉化成證AE=AC．
證明：過C作CE∥DA，交BA的延長線于E．
CE∥DA?
∠1=∠E
∠2=∠3
∠1=∠2
?∠E=∠3?AE=AC，
CE∥DA?
BD
DC
=
BA
AE
AE=AC
?
BD
DC
=
AB
AC

（1）上述證明過程中，用到了哪些定理？（寫對兩個定理即可）
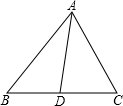（2）在上述分析、證明過程中，主要用到了下列三種數學思想的哪一種？選出一個填在后面的括號內．精英家教網[]
①數形結合思想；
②轉化思想；
③分類討論思想．
（3）用三角形內角平分線性質定理解答問題：
已知：如圖，△ABC中，AD是角平分線，AB=5cm，AC=4cm，BC=7cm．求BD的長．

查看答案和解析>>

科目：初中數學 來源：期末題 題型：解答題

閱讀下面材料，按要求完成后面作業。
三角形內角平分線性質定理：三角形內角平分線分對邊所得的兩條線段和這個角的兩邊對應成比例。
 已知：△ABC中，AD是角平分線（如圖1）， 求證：=。
               
分析：要證=，一般只要證BD、DC與AB、AC或BD、AB與DC、AC所在的三角形相似，現在B、D、C在一條直線，△ABD與△ADC不相似，需要考慮用別的方法換比。
 在比例式=中，AC恰好是BD、DC、AB的第四比例項，所以考慮過C作CE∥AD交BA的延長線于E，從而得到BD、DC、AB的第四比例項AE，這樣，證明=，就可轉化證=。
（1）完成證明過程： 
證明：
（2）上述證明過程中，用到了哪些定理（寫對兩個即可）
答：用了：①____________；
②_____________。
 （3）在上述分析和你的證明過程中，主要用到了下列三種數學思想的哪一種：①數形結合思想 ②轉化思想 ③分類討論思想　
答：____________。
（4） 用三角形內角平分線定理解答問題：　
如圖2，△ABC中，AD是角平分線，AB=5cm，AC=4cm，BD=7cm，求BC之長。

查看答案和解析>>

科目：初中數學 來源：2000年全國中考數學試題匯編《圖形的相似》（03）（解析版） 題型：解答題

（2000•山西）請閱讀下面材料，并回答所提出的問題．
三角形內角平分線性質定理：三角形的內角平分線分對邊所得的兩條線段和這個角的兩邊對應成比例．
已知：如圖，△ABC中，AD是角平分線．
求證：
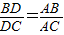
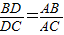分析：要證，一般只要證BD、DC與AB、AC或BD、AB與DC、AC所在三角形相似．現在B、D、C在一直線上，△ABD與△ADC不相似，需要考慮用別的方法換比．在比例式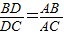中，AC恰是BD、DC、AB的第四比例項，所以考慮過C作CE∥AD，交BA的延長線于E，從而得到BD、DC、AB的第四比例項AE，這樣，證明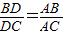就可以轉化成證AE=AC．
證明：過C作CE∥DA，交BA的延長線于E．
CE∥DA，
CE∥DA
（1）上述證明過程中，用到了哪些定理？（寫對兩個定理即可）
（2）在上述分析、證明過程中，主要用到了下列三種數學思想的哪一種？選出一個填在后面的括號內．[]
①數形結合思想；
②轉化思想；
③分類討論思想．
（3）用三角形內角平分線性質定理解答問題：
已知：如圖，△ABC中，AD是角平分線，AB=5cm，AC=4cm，BC=7cm．求BD的長．

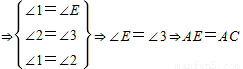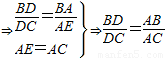
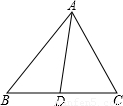
查看答案和解析>>

科目：初中數學 來源：2000年全國中考數學試題匯編《三角形》（05）（解析版） 題型：解答題

（2000•山西）請閱讀下面材料，并回答所提出的問題．
三角形內角平分線性質定理：三角形的內角平分線分對邊所得的兩條線段和這個角的兩邊對應成比例．
已知：如圖，△ABC中，AD是角平分線．
求證：
分析：要證，一般只要證BD、DC與AB、AC或BD、AB與DC、AC所在三角形相似．現在B、D、C在一直線上，△ABD與△ADC不相似，需要考慮用別的方法換比．在比例式中，AC恰是BD、DC、AB的第四比例項，所以考慮過C作CE∥AD，交BA的延長線于E，從而得到BD、DC、AB的第四比例項AE，這樣，證明就可以轉化成證AE=AC．
證明：過C作CE∥DA，交BA的延長線于E．
CE∥DA，
CE∥DA
（1）上述證明過程中，用到了哪些定理？（寫對兩個定理即可）
（2）在上述分析、證明過程中，主要用到了下列三種數學思想的哪一種？選出一個填在后面的括號內．[]
①數形結合思想；
②轉化思想；
③分類討論思想．
（3）用三角形內角平分線性質定理解答問題：
已知：如圖，△ABC中，AD是角平分線，AB=5cm，AC=4cm，BC=7cm．求BD的長．

查看答案和解析>>

科目：初中數學 來源：2000年全國中考數學試題匯編《相交線與平行線》（01）（解析版） 題型：解答題

（2000•山西）請閱讀下面材料，并回答所提出的問題．
三角形內角平分線性質定理：三角形的內角平分線分對邊所得的兩條線段和這個角的兩邊對應成比例．
已知：如圖，△ABC中，AD是角平分線．
求證：
分析：要證，一般只要證BD、DC與AB、AC或BD、AB與DC、AC所在三角形相似．現在B、D、C在一直線上，△ABD與△ADC不相似，需要考慮用別的方法換比．在比例式中，AC恰是BD、DC、AB的第四比例項，所以考慮過C作CE∥AD，交BA的延長線于E，從而得到BD、DC、AB的第四比例項AE，這樣，證明就可以轉化成證AE=AC．
證明：過C作CE∥DA，交BA的延長線于E．
CE∥DA，
CE∥DA
（1）上述證明過程中，用到了哪些定理？（寫對兩個定理即可）
（2）在上述分析、證明過程中，主要用到了下列三種數學思想的哪一種？選出一個填在后面的括號內．[]
①數形結合思想；
②轉化思想；
③分類討論思想．
（3）用三角形內角平分線性質定理解答問題：
已知：如圖，△ABC中，AD是角平分線，AB=5cm，AC=4cm，BC=7cm．求BD的長．

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 成人免费淫片aa视频免费 | www.久久久.com| 亚洲在线观看免费视频 | 日韩亚洲欧美在线观看 | 色婷婷av一区二区三区软件 | 国产又粗又猛视频免费 | 精品一二区 | 欧美 日韩 国产 一区 | 黄色av影院| 精品三级在线观看 | 精品亚洲网 | 日韩一二三区在线观看 | 日韩二区 | 亚洲 欧美 日韩 在线 | 国产精品一区二区三区四区 | 日韩在线视频观看 | 韩日精品在线观看 | 精品视频免费 | 久久免费精品视频 | 国产区 在线观看 | 免费看片色 | 日韩天堂 | 精品国产不卡一区二区三区 | 一级视频在线免费观看 | 综合色成人 | 国产精品免费视频观看 | 精品久久久久久国产 | www.欧美日韩 | 国产精品日韩欧美一区二区三区 | 日韩素人在线 | 中文字幕不卡 | 天天澡天天狠天天天做 | 久久久精选 | 国产在线不卡一区 | 69久久99精品久久久久婷婷 | 国产一区二精品区在线 | 美国一级黄色片 | 久久精品久久久久久久久久久久久 | 欧美lesbianxxxxhd视频社区 | 国产高清免费 | 欧美日韩不卡在线 |