
【題目】如圖,平面直角坐標系中,一次函數![]() 的圖象與
的圖象與![]() 軸交于點
軸交于點![]() .
.
(1)若點![]() 關于
關于![]() 軸的對稱點
軸的對稱點![]() 在一次函數
在一次函數![]() 的圖象上,求
的圖象上,求![]() 的值;
的值;
(2)求由直線![]() ,(1)中的直線
,(1)中的直線![]() 以及
以及![]() 軸圍成的三角形的面積.
軸圍成的三角形的面積.
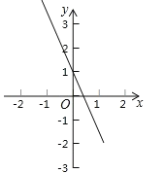
科目:初中數學 來源: 題型:
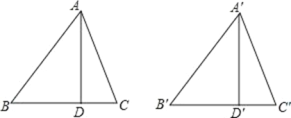
【題目】如圖,銳角三角形 ABC 和銳角三角形 A'B'C'中,AD、A'D'分別是邊 BC、B'C'上的高,且AB=A'B',AD=A'D'.要使△ABC≌△A'B'C',則應補充條件:________(填寫一個即可)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在數軸上,點O為原點,點A表示的數為a,點B表示的數為b,且a,b滿足![]()
![]() ,B兩點對應的數分別為
,B兩點對應的數分別為![]() ______,
______,![]() ______;
______;
![]() 若將數軸折疊,使得A點與B點重合,則原點O與數______表示的點重合;
若將數軸折疊,使得A點與B點重合,則原點O與數______表示的點重合;
![]() 若點A、B分別以4個單位
若點A、B分別以4個單位![]() 秒和3個單位
秒和3個單位![]() 秒的速度相向而行,則幾秒后A、B兩點相距1個單位長度?
秒的速度相向而行,則幾秒后A、B兩點相距1個單位長度?
![]() 若點A、B以
若點A、B以![]() 中的速度同時向右運動,點P從原點O以7個單位
中的速度同時向右運動,點P從原點O以7個單位![]() 秒的速度向右運動,是否存在常數m,使得
秒的速度向右運動,是否存在常數m,使得![]() 為定值,若存在,請求出m值以及這個定值;若不存在,請說明理由.
為定值,若存在,請求出m值以及這個定值;若不存在,請說明理由.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖,在△ABC中,∠B=40°,∠C=80°,AD⊥BC于D,且AE平分∠BAC,求∠EAD的度數.
(2)上題中若∠B=40°,∠C=80°改為∠C>∠B,其他條件不變,請你求出∠EAD與∠B、∠C之間的數列關系?并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】AD是△ABC的高,AC=2 ![]() ,AD=4,把△ADC沿著直線AD對折,點C落在點E的位置,如果△ABE是等腰三角形,那么線段BE的長度為( )
,AD=4,把△ADC沿著直線AD對折,點C落在點E的位置,如果△ABE是等腰三角形,那么線段BE的長度為( )
A.2 ![]()
B.2 ![]() 或5
或5
C.2 ![]()
D.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,方格中,每個小正方形的邊長都是單位1,△ABC在平面直角坐標系中的位置如圖.
(1)①畫出△ABC關于y軸對稱的△A1B1C1;
②畫出△ABC繞點O按順時針方向旋轉90°后的△A2B2C2;
(2)判斷△A1B1C1和△A2B2C2是不是成軸對稱?如果是,請在圖中作出它們的對稱軸.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校組織學生參觀航天展覽,甲、乙、丙、丁四位同學隨機分成兩組乘車.
(1)哪兩位同學會被分到第一組,寫出所有可能;
(2)用列表法(或樹狀圖法)求甲、乙分在同一組的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,將1張菱形紙片ABC的(∠ADC>90°)沿對角線BD剪開,得到△ABD和△BCD.再將△BCD以D為旋轉中心,按逆時針方向旋轉角α,使α=∠ADB,得到如圖2所示的△DB′C,連接AC、BB′,∠DAB=45°,有以下結論:①AC=BB′;②AC⊥AB;③∠CDA=90°;④BB′= ![]() AB,其中正確結論的序號是 . (把所有正確結論的序號都填在橫線上)
AB,其中正確結論的序號是 . (把所有正確結論的序號都填在橫線上) 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對任意一個三位數n,如果n滿足各個數位上的數字互不相同,且都不為零,那么稱這個數為“相異數”,將一個“相異數”任意兩個數位上的數字對調后可以得到三個不同的新三位數,把這三個新三位數的和與111的商記為F(n).例如n=123,對調百位與十位上的數字得到213,對調百位與個位上的數字得到321,對調十位與個位上的數字得到132,這三個新三位數的和為213+321+132=666,666÷111=6,所以F(123)=6.
(1)計算:F(243),F(617);
(2)若s,t都是“相異數”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整數),規定:k= ![]() ,當F(s)+F(t)=18時,求k的最大值.
,當F(s)+F(t)=18時,求k的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com