
【題目】如圖,在正方形![]() 中,
中,![]() 、
、![]() 分別是邊
分別是邊![]() 、
、![]() 上的點,且
上的點,且![]() ,
,![]() 與
與![]() 相交于點
相交于點![]() ,則圖中與
,則圖中與![]() 相似的三角形有________.
相似的三角形有________.

【答案】![]() ,
,![]() ,
,![]()
【解析】
利用正方形的性質,運用SAS證明△ABF≌△DAE,再由全等三角形的性質可得出答案.
∵四邊形ABCD是正方形,
∴AB=AD,∠BAF=∠ADE=90°.
∵CE=DF,
∴AF=DE.
在△ABF與△DAE中,
∵ ,
,
∴△ABF≌△DAE(SAS).
∴AE=BF;
∴∠AFB=∠AED.
∵∠AED+∠DAE=90°,
∴∠AFB+∠DAE=90°,
∴∠AOF=90°,即AE⊥BF.
∵∠BAF=90°,
∴∠AFB+∠ABF=90°.
∵∠ABF+∠BAM=90°,
∴∠BAM=∠AFM,
∴△ABM∽△FAM.
同理,△ABM∽△FBA.△ABM∽△AED
故答案為:△ABM∽△FAM,△ABM∽△FBA,△ABM∽△AED.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖①,二次函數的拋物線的頂點坐標C,與x軸的交于A(1,0)、B(﹣3,0)兩點,與y軸交于點D(0,3).

(1)求這個拋物線的解析式;
(2)如圖②,過點A的直線與拋物線交于點E,交y軸于點F,其中點E的橫坐標為﹣2,若直線PQ為拋物線的對稱軸,點G為直線PQ上的一動點,則x軸上是否存在一點H,使D、G、H、F四點所圍成的四邊形周長最小?若存在,求出這個最小值及點G、H的坐標;若不存在,請說明理由;
(3)如圖③,連接AC交y軸于M,在x軸上是否存在點P,使以P、C、M為頂點的三角形與△AOM相似?若存在,求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
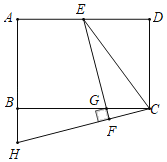
【題目】如圖,在長方形ABCD中,點E是AD的中點,連接CE,將△CDE沿著CE翻折得到△CFE,EF交BC于點G,CF的延長線交AB的延長線于點H,若AH=25,BC=40,則FG=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在學習《實數》內容時,我們估算帶有根號的無理數的近似值時,經常使用“逐步逼近”的方法來實現的.“逐步逼近”是數學思維方法的一種重要形式,主要通過構造“擬對象”、逐步擴充元素、逐步擴充范圍、放縮逼近、合力逼近等方式解決問題.
例如:估算![]() 的近似值時,利用“逐步逼近”法可以得出
的近似值時,利用“逐步逼近”法可以得出![]() .請你根據閱讀內容回答下列問題:
.請你根據閱讀內容回答下列問題:
(1)![]() 介于連續的兩個整數
介于連續的兩個整數![]() 和
和![]() ,且
,且![]() ,那么
,那么![]() ______,
______,![]() ______;
______;
(2)![]() 的整數部分是______,小數部分是______;
的整數部分是______,小數部分是______;
(3)已知![]() 的小數部分為
的小數部分為![]() ,
,![]() 的小數部分為
的小數部分為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《鄭州市城市生活垃圾分類管理辦法》已于2019年12月1日起施行,為了解市民對垃圾分類的執行程度,某數學興趣小組對部分市民進行了問卷調查,調查結果分為“A完全做到”“B基本做到”“C偶爾做到”“D很少做到”四類,該小組繪制的統計圖如右:

(1)圖中最大的扇形表示調查結果為 的市民占所有被調查市民的 %,這個扇形的圓心角為 °;
(2)你從圖中還能得到哪些信息?(寫出一條即可)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形![]() 中,對角線
中,對角線![]() ,
,![]() 相交于點
相交于點![]() ,且
,且![]() ,
,![]() ,動點
,動點![]() ,
,![]() 分別從點
分別從點![]() ,
,![]() 同時出發,運動速度均為
同時出發,運動速度均為![]() ,點
,點![]() 沿
沿![]() 運動,到點
運動,到點![]() 停止,點
停止,點![]() 沿
沿![]() 運動,到點
運動,到點![]() 停止
停止![]() 后繼續運動,到點
后繼續運動,到點![]() 停止,連接
停止,連接![]() ,
,![]() ,
,![]() .設
.設![]() 的面積為
的面積為![]() (這里規定:線段是面積
(這里規定:線段是面積![]() 的幾何圖形),點
的幾何圖形),點![]() 的運動時間為
的運動時間為![]() .
.
![]() 填空:
填空:![]() ________
________![]() ,
,![]() 與
與![]() 之間的距離為________
之間的距離為________![]() ;
;
![]() 當
當![]() 時,求
時,求![]() 與
與![]() 之間的函數解析式;
之間的函數解析式;
![]() 直接寫出在整個運動過程中,使
直接寫出在整個運動過程中,使![]() 與菱形
與菱形![]() 一邊平行的所有
一邊平行的所有![]() 的值.
的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC的三邊長分別為3,4,5,△DEF的三邊長分別為3,3x﹣2,2x+1,若這兩個三角形全等,則x的值為( )
A. 2 B. 2或![]() C.
C. ![]() 或
或![]() D. 2或
D. 2或![]() 或
或![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】銅陵市義安區實施了城鄉居民基本醫療保險(簡稱“醫療保險”),辦法規定農村村民只要每人每年交納180元錢就可以加入醫療保險,住院時自己先墊付,出院同時就可得到按一定比例的報銷款,這項舉措惠及民生,吳斌與同學隨機調查了他們鎮的一些農民,根據收集到的數據繪制了以下的統計圖.
根據圖中信息,解答下列問題:
(1)本次調查了多少村民?被調查的村民中參加醫療保險,得到報銷款的有多少人?
(2)若該鎮有34000村民,請估算有多少人參加了醫療保險?要使兩年后參加醫療保險的人數增加到業務31460人,假設這兩年的年增長率相同,求年增長率?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com