
【題目】如圖,點A是直線AM與⊙O的交點,點B在⊙O上,BD⊥AM垂足為D,BD與⊙O交于點C,OC平分∠AOB,∠B=60°.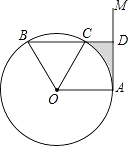
(1)求證:AM是⊙O的切線;
(2)若DC=2,求圖中陰影部分的面積(結果保留π和根號).
【答案】
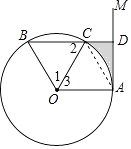
(1)
解:∵∠B=60°,
∴△BOC是等邊三角形,
∴∠1=∠2=60°,
∵OC平分∠AOB,
∴∠1=∠3,
∴∠2=∠3,
∴OA∥BD,
∴∠BDM=90°,∴∠OAM=90°,
∴AM是⊙O的切線
(2)
解:∵∠3=60°,OA=OC,
∴△AOC是等邊三角形,
∴∠OAC=60°,
∵∠OAM=90°,
∴∠CAD=30°,
∵CD=2,
∴AC=2CD=4,
∴AD=2 ![]() ,
,
∴S陰影=S梯形OADC﹣S扇形OAC= ![]() (4+2)×2
(4+2)×2 ![]() ﹣
﹣ ![]() =6
=6 ![]() ﹣
﹣ ![]()
【解析】(1)由已知條件得到△BOC是等邊三角形,根據等邊三角形的性質得到∠1=∠2=60°,由角平分線的性質得到∠1=∠3,根據平行線的性質得到∠OAM=90°,于是得到結論;(2)根據等邊三角形的性質得到∠OAC=60°,根據三角形的內角和得到∠CAD=30°,根據勾股定理得到AD=2 ![]() ,于是得到結論.
,于是得到結論.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,將半徑為2,圓心角為120°的扇形OAB繞點A逆時針旋轉60°,點O,B的對應點分別為O′,B′,連接BB′,則圖中陰影部分的面積是( ) 
A.![]()
B.2 ![]() ﹣
﹣ ![]()
C.2 ![]() ﹣
﹣ ![]()
D.4 ![]() ﹣
﹣ ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
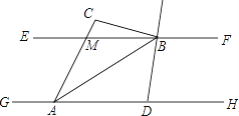
【題目】如圖,已知EF∥GH,A、D為GH上的兩點,M、B為EF上的兩點,延長AM于點C,AB平分∠DAC,直線DB平分∠FBC,若∠ACB=100°,則∠DBA的度數為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把下列各數分別填入相應的集合內:
﹣2.5,0,8,﹣2,![]() ,
,![]() , ﹣0.5252252225…(每兩個5之間依次增加1個2).
, ﹣0.5252252225…(每兩個5之間依次增加1個2).
(1)正數集合:{ …};
(2)負數集合:{ …};
(3)整數集合:{ …};
(4)無理數集合:{ …}.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某重點中學校團委、學生會發出倡議,在初中各年級捐款購買書籍送給我市貧困地區的學校.初一年級利用捐款買甲、乙兩種自然科學書籍若干本,用去5324元;初二年級買了A、B兩種文學書籍若干本,用去4840元,其中A、B的數量分別與甲、乙的數量相等,且甲種書與B種書的單價相同,乙種書與A種書的單價相同.若甲、乙兩種書的單價之和為121元,則初一和初二兩個年級共向貧困地區的學校捐獻了________本書.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明一家利用國慶八天駕車到某景點旅游,小汽車出發前油箱有油35L,行駛若干小時后,途中在加油站加油若干升,油箱中余油量Q(L)與行駛時間t(h)之間的關系如圖所示,根據圖像回答下列問題:
(1)小汽車行駛______h后加油,中途加油_______L
(2)求加油前油箱余油量Q與行駛時間t的函數關系式
(3)如果小汽車在行駛過程中耗油量速度不變,加油站距景點200km,車速80km/h,要到達目的地,油箱中的油是否夠用?請說明理由

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點C,E,F,B在同一直線上,點A,D在BC異側,AB∥CD,AE=DF,∠A=∠D.
(1)求證:AB=CD;
(2)若AB=CF,∠B=40°,求∠D的度數.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com