
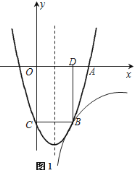
【題目】如圖![]() ,二次函數
,二次函數![]() 的圖象與
的圖象與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,過點
,過點![]() 作
作![]() 軸,交拋物線于點
軸,交拋物線于點![]() ,并過點
,并過點![]() 作
作![]() 軸,垂足為
軸,垂足為![]() .拋物線
.拋物線![]() 和反比例函數
和反比例函數![]() 的圖象都經過點
的圖象都經過點![]() ,四邊形
,四邊形![]() 的面積是
的面積是![]() .
.
![]() 求反比例函數、二次函數的解析式及拋物線的對稱軸;
求反比例函數、二次函數的解析式及拋物線的對稱軸;
![]() 如圖
如圖![]() ,點
,點![]() 從
從![]() 點出發以每秒
點出發以每秒![]() 個單位的速度沿線段
個單位的速度沿線段![]() 向
向![]() 點運動,點
點運動,點![]() 從
從![]() 點出發以相同的速度沿線段img src="http://thumb.zyjl.cn/questionBank/Upload/2019/05/12/08/1a8f9afd/SYS201905120854095644903087_ST/SYS201905120854095644903087_ST.023.png" width="24" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />向
點出發以相同的速度沿線段img src="http://thumb.zyjl.cn/questionBank/Upload/2019/05/12/08/1a8f9afd/SYS201905120854095644903087_ST/SYS201905120854095644903087_ST.023.png" width="24" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />向![]() 點運動,其中一個動點到達端點時,另一個也隨之停止運動.設運動時間為
點運動,其中一個動點到達端點時,另一個也隨之停止運動.設運動時間為![]() 秒.
秒.
①當![]() 為何值時,四邊形
為何值時,四邊形![]() 為等腰梯形;
為等腰梯形;
②設![]() 與對稱軸的交點為
與對稱軸的交點為![]() ,過
,過![]() 點作
點作![]() 軸的平行線交
軸的平行線交![]() 于點
于點![]() ,設四邊形
,設四邊形![]() 的面積為
的面積為![]() ,求面積
,求面積![]() 關于時間
關于時間![]() 的函數解析式,并指出
的函數解析式,并指出![]() 的取值范圍;當
的取值范圍;當![]() 為何值時,
為何值時,![]() 有最大值或最小值.
有最大值或最小值.

【答案】![]()
![]() ,
,![]() ①當
①當![]() 秒時,四邊形
秒時,四邊形![]() 為等腰梯形②當
為等腰梯形②當![]() 秒時,面積
秒時,面積![]() 有最小值
有最小值![]() .
.
【解析】
(1)根據反比例函數的比例系數k的幾何意義可求出k,從而可求出點B的坐標,然后運用待定系數法就可求出二次函數的解析式,由此可求出對稱軸方程;
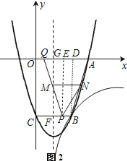
(2)①過點P作PE⊥OA,垂足為E,如圖2,易證BC∥OA,要使四邊形ABPQ為等腰梯形,只需PQ=AB,只需QE=AD=1,由此即可求出t的值;②如圖2,易證△MFP≌△MGQ,則有MF=MG,從而可求出S△BPN(用t表示),然后只需求出S四邊形ABPQ,并運用割補法就可得到S關于t的函數解析式,然后只需利用該函數的增減性就可解決問題.
![]() 如圖
如圖![]() ,
,
∵四邊形![]() 的面積是
的面積是![]()
,
∴![]() ,
,
∴反比例函數的解析式為![]() .
.
∵反比例函數![]() 的圖象經過點
的圖象經過點![]() ,
,
∴![]() ,
,
解得![]() .
.
∴![]() .
.
將點![]() ,
,![]() 代入
代入![]() ,得
,得
![]()
解得:![]() ,
,
∴二次函數的解析式![]() .
.
則拋物線的對稱軸為![]() ;
;![]() ①由題意可知:
①由題意可知:![]() .
.
∵點![]() ,點
,點![]() 的縱坐標相等,
的縱坐標相等,
∴![]() .
.
過點![]() 作
作![]() ,垂足為
,垂足為![]() ,如圖
,如圖![]() .
.
要使四邊形![]() 為等腰梯形,只需
為等腰梯形,只需![]() .
.
即![]() .
.
又![]() ,
,
∴![]() .
.
解得![]() ,
,
∴當![]() 秒時,四邊形
秒時,四邊形![]() 為等腰梯形.
為等腰梯形.
②設對稱軸與![]() 、
、![]() 軸的交點分別為
軸的交點分別為![]() 、
、![]() ,如圖
,如圖![]() .
.
∵對稱軸![]() 是線段
是線段![]() 的垂直平分線,
的垂直平分線,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
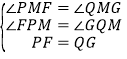
∴![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]() .
.
∵![]()
![]()
![]() ,
,
∴![]()
![]() .
.
∵![]() ,
,![]() ,
,
∴點![]() 運動到點
運動到點![]() 時停止運動,需要
時停止運動,需要![]() 秒,
秒,
∴![]() .
.
∵![]() ,
,
∴當![]() 秒時,面積
秒時,面積![]() 有最小值
有最小值![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】甲乙兩位同學用圍棋子做游戲.如圖所示,現輪到黑棋下子,黑棋下一子后白棋再下一子,使黑棋的![]() 個棋子組成軸對稱圖形,白棋的
個棋子組成軸對稱圖形,白棋的![]() 個棋子也成軸對稱圖形.則下列下子方法不正確的是( ),
個棋子也成軸對稱圖形.則下列下子方法不正確的是( ),![]() .
.

A. 黑(3,7);白(5,3) B. 黑(4,7);白(6,2)
C. 黑(2,7);白(5,3) D. 黑(3,7);白(2,6)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,邊長為24的等邊三角形ABC中,M是高CH所在直線上的一個動點,連結MB,將線段BM繞點B逆時針旋轉60°得到BN,連結HN.則在點M運動過程中,線段HN長度的最小值是( )

A. 12B. 6C. 3D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)問題探究:如圖①,在四邊形ABCD中,AB∥CD,E是BC的中點,AE是∠BAD的平分線,則線段AB,AD,DC之間的等量關系為 ;
(2)方法遷移:如圖②,在四邊形ABCD中,AB∥CD,AF與DC的延長線交于點F,E是BC的中點,AE是∠BAF的平分線,試探究線段AB,AF,CF之間的等量關系,并證明你的結論;
(3)聯想拓展:如圖③,AB∥CF,E是BC的中點,點D在線段AE上,∠EDF=∠BAE,試探究線段AB,DF,CF之間的數量關系,并證明你的結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著近幾年我市私家車日越增多,超速行駛成為引發交通事故的主要原因之一.某中學數學活動小組為開展“文明駕駛、關愛家人、關愛他人”的活動,設計了如下檢測公路上行駛的汽車速度的實驗:先在公路旁邊選取一點![]() ,在筆直的車道
,在筆直的車道![]() 上確定點
上確定點![]() ,使
,使![]() 和
和![]() 垂直,測得
垂直,測得![]() 的長等于
的長等于![]() 米,在
米,在![]() 上的同側取點
上的同側取點![]() 、
、![]() ,使
,使![]() ,
,![]() .
.

![]() 求
求![]() 、
、![]() 之間的路程(保留根號);
之間的路程(保留根號);
![]() 已知本路段對校車限速為
已知本路段對校車限速為![]() 米/秒若測得某校車從
米/秒若測得某校車從![]() 到
到![]() 用了
用了![]() 秒,這輛校車是否超速?請說明理由.
秒,這輛校車是否超速?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面直角坐標系的原點![]() 是正方形
是正方形![]() 的中心,頂點
的中心,頂點![]() ,
,![]() 的坐標分別為
的坐標分別為![]() 、
、![]() ,把正方形
,把正方形![]() 繞原點
繞原點![]() 逆時針旋轉
逆時針旋轉![]() 得到正方形
得到正方形![]() ,則正方形
,則正方形![]() 與正方形
與正方形![]() 重疊部分形成的正八邊形的邊長為( )
重疊部分形成的正八邊形的邊長為( )

A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】課上老師呈現一個問題:

下面提供三種思路:
思路一:過點F作MN∥CD(如圖甲);
思路二:過P作PN∥EF,交AB于點N;
思路三:過O作ON∥FG,交CD于點N.
解答下列問題:

(1)根據思路一(圖甲),可求得∠EFG的度數為 ;
(2)根據思路二、三分別在圖乙和圖丙中作出符合要求的輔助線;
(3)請你從思路二、思路三中任選其中一種,寫出求∠EFG度數的解答過程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com