
【題目】如圖,在△ABC中,∠C=90°,AE平分∠BAC交BC于點E,O是AB上一點,經過A,E兩點的⊙O交AB于點D,連接DE,作∠DEA的平分線EF交⊙O于點F,連接AF.
(1)求證:BC是⊙O的切線;
(2)若sin∠EFA=![]() ,AF=
,AF=![]() ,求線段AC的長.
,求線段AC的長.

【答案】(1)證明見解析;(2)6.4.
【解析】
(1)連接OE,根據等腰三角形的性質和角平分線定義可得![]() ,根據平行線的判定可得OE∥AC,再由平行線的性質可得∠BEO=∠C=90°,即可證得結論;(2)連接
,根據平行線的判定可得OE∥AC,再由平行線的性質可得∠BEO=∠C=90°,即可證得結論;(2)連接![]() ,根據已知條件易證
,根據已知條件易證![]() .在
.在![]() 中,根據勾股定理求得
中,根據勾股定理求得![]() .根據同弧所對的圓周角相等及已知條件可得
.根據同弧所對的圓周角相等及已知條件可得![]() .在
.在![]() 中求得AE的長,再證明ΔACE∽ΔAED,根據相似三角形的性質即可求得線段AC的長.
中求得AE的長,再證明ΔACE∽ΔAED,根據相似三角形的性質即可求得線段AC的長.
證明:(1)如圖1,連接![]() ,
,
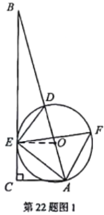
∵![]() ,
,
∴![]() .
.
∵![]() 平分
平分![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() ∥
∥![]() ,
,
∴![]() .
.
∴![]()
∵![]() 為
為![]() 的半徑,
的半徑,
∴![]() 是
是![]() 的切線.
的切線.
(2)如圖2,連接![]() .
.
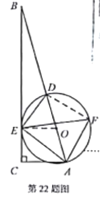
由題可知![]() 為
為![]() 的直徑,
的直徑,
∴![]() .
.
∵![]() 平分
平分![]() ,
,
∴![]() .
.
∴![]() .
.
∴△AFD為等腰直角三角形,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ∽
∽![]() .
.
∴![]() .
.
∴![]() (或6.4)
(或6.4)


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
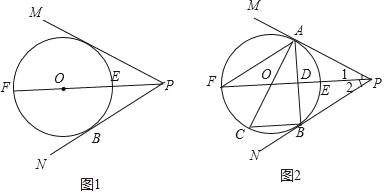
【題目】如圖1,已知∠MPN的角平分線PF經過圓心O交⊙O于點E、F,PN是⊙O的切線,B為切點.
(1)求證:PM也是⊙O的切線;
(2)如圖2,在(1)的前提下,設切線PM與⊙O的切點為A,連接AB交PF于點D;連接AO交⊙O于點C,連接BC,AF;記∠PFA為∠α.
①若BC=6,tan∠α=![]() ,求線段AD的長;
,求線段AD的長;
②小華探究圖2之后發現:EF2=mODOP(m為正整數),請你猜想m的數值?并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中
中![]() ,
,![]() ,點
,點![]() 在
在![]() 邊上,
邊上,![]() 于點
于點![]() .
.

![]() 若
若![]() ,
,![]() ,求
,求![]() 的長;
的長;
![]() 設點
設點![]() 在線段
在線段![]() 上,點
上,點![]() 在射線
在射線![]() 上,以
上,以![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 有一個銳角相等,
有一個銳角相等,![]() 交
交![]() 于點
于點![]() .問:線段
.問:線段![]() 可能是
可能是![]() 的高線還是中線?或兩者都有可能?請說明理由.
的高線還是中線?或兩者都有可能?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,射線OM在第一象限,且與x軸正半軸的夾角為60°,過點D(6,0)作DA⊥OM于點A,作線段 OD的垂直平分線BE交x軸于點E,交AD于點B,作射線OB.以AB為邊在△AOB的外側作正方形ABCA1,延長A1C交射線OB于點B1,以A1B1為邊在△A1OB1的外側作正方形A1B1C1A2,延長A2C1交射線OB于點B2,以A2B2為邊在△A2OB2的外側作正方形A2B2C2A3……按此規律進行下去,則正方形A2017B2017C2017A2018的周長為______________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】動畫片《小豬佩奇》分靡全球,受到孩子們的喜愛.現有4張《小豬佩奇》角色卡片,分別是A佩奇,B喬治,C佩奇媽媽,D佩奇爸爸(四張卡片除字母和內容外,其余完全相同).姐弟兩人做游戲,他們將這四張卡片混在一起,背面朝上放好.
(1)姐姐從中隨機抽取一張卡片,恰好抽到A佩奇的概率為 ;
(2)若兩人分別隨機抽取一張卡片(不放回),請用列表或畫樹狀圖的分方法求出恰好姐姐抽到A佩奇弟弟抽到B喬治的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,以□ABCD的較短邊CD為一邊作菱形CDEF,使點F落在邊AD上,連接BE,交AF于點G.
(1)猜想BG與EG的數量關系.并說明理由;
(2)延長DE,BA交于點H,其他條件不變,
①如圖2,若∠ADC=60°,求![]() 的值;
的值;
②如圖3,若∠ADC=α(0°<α<90°),直接寫出![]() 的值.(用含α的三角函數表示)
的值.(用含α的三角函數表示)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC=4,∠ABC和∠ACB的平分線交于點E,過點E作MN∥BC分別交AB、AC于M、N,則△AMN的周長為______________

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,MN表示某引水工程的一段設計路線,從點M到點N的走向為北偏西30°,在點M的北偏西60°方向上有一點A,以點A為圓心,以500米為半徑的圓形區域為居民區,取MN上另一點B,測得BA的方向為北偏西75°.已知MB=400米,若不改變方向,則輸水路線是否會穿過居民區?請通過計算說明理由.(參考數據: ![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】城南中學九年級共有12個班,每班48名學生,學校對該年級學生數學學科學業水平測試成績進行了抽樣分析,請按要求回答下列問題:
(1)(收集數據)要從九年級學生中抽取一個48人的樣本,你認為以下抽樣方法中最合理的是________.
①隨機抽取一個班級的48名學生;②在九年級學生中隨機抽取48名女學生;③在九年級12個班中每班各隨機抽取4名學生.
(2)(整理數據)將抽取的48名學生的成績進行分組,繪制成績頻數分布表和成績分布扇形統計圖如下.
請根據圖表中數據填空:
①表中m的值為________;
② B類部分的圓心角度數為________°;
③估計C、D類學生大約一共有________名.

九年級學生數學成績頻數分布表
成績(單位:分) | 頻數 | 頻率 |
A類(80~100) | 24 |
|
B類(60~79) | 12 |
|
C類(40~59) | 8 | m |
D類(0~39) | 4 |
|
(3)(分析數據)教育主管部們為了解學校學生成績情況,將同層次的城南、城北兩所中學的抽樣數據進行對比分析,得到下表:
學校 | 平均數(分) | 方差 | A、B類的頻率和 |
城南中學 | 71 | 358 | 0.75 |
城北中學 | 71 | 588 | 0.82 |
請你評價這兩所學校學生數學學業水平測試的成績,提出一個解釋來支持你的觀點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com