
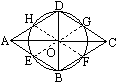
求證:菱形四條邊的中點在以對角線交點為圓心的同一個圓上.
已知:如圖所示,菱形ABCD的對角線AC和BD相交于點O,而點E,F,G,H分別是AB,BC,CD,DA的中點.求證:E,F,G,H在以點O為圓心的同一個圓上.
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
查看答案和解析>>
科目:初中數學 來源: 題型:
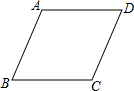 我們知道,小學對菱形的認識是:四條邊都相等的四邊形.到了初中,對菱形的定義是:有一組鄰邊相等的平行四邊形,請你利用初中的定義來說明小學認識的合理性.先補全題目,再完成證明:
我們知道,小學對菱形的認識是:四條邊都相等的四邊形.到了初中,對菱形的定義是:有一組鄰邊相等的平行四邊形,請你利用初中的定義來說明小學認識的合理性.先補全題目,再完成證明:查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2011年安徽省馬鞍山市成功學校中考數學一模試卷(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com