【題目】如圖，
是⊙
的直徑，
是⊙上一點，
，垂足為
、
、
分別是
、
上一點（不與端點重合），如果
，下面結論：①
；②
；③
；④
；⑤
．其中正確的是（ ）
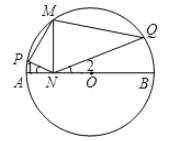
A. ①②③B. ①③⑤C. ④⑤D. ①②⑤
科目：初中數學 來源： 題型：
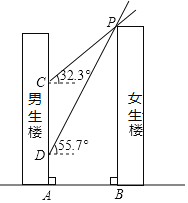
【題目】如圖，男生樓在女生樓的左側，兩樓高度均為90m，樓間距為AB，冬至日正午，太陽光線與水平面所成的角為
，女生樓在男生樓墻面上的影高為CA；春分日正午，太陽光線與水平面所成的角為
，女生樓在男生樓墻面上的影高為DA，已知
．
求樓間距AB；
若男生樓共30層，層高均為3m，請通過計算說明多少層以下會受到擋光的影響？
參考數據：
，
，
，
，
，
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知拋物線y＝﹣x2+bx+c經過點B（﹣1，0）和點C（2，3）．
（1）求此拋物線的函數表達式；
（2）如果此拋物線上下平移后過點（﹣2，﹣1），試確定平移的方向和平移的距離．
查看答案和解析>>
科目：初中數學 來源： 題型：
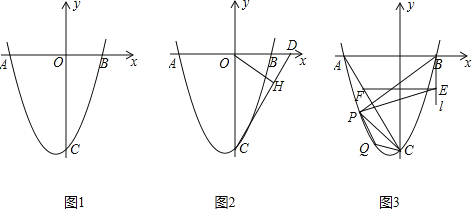
【題目】如圖1，拋物線
交x軸于點
，
，交y軸于點C．
求拋物線的解析式；
如圖2，D點坐標為
，連結
若點H是線段DC上的一個動點，求
的最小值．
如圖3，連結AC，過點B作x軸的垂線l，在第三象限中的拋物線上取點P，過點P作直線AC的垂線交直線l于點E，過點E作x軸的平行線交AC于點F，已知
．
求點P的坐標；
在拋物線上是否存在一點Q，使得
成立？若存在，求出Q點坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
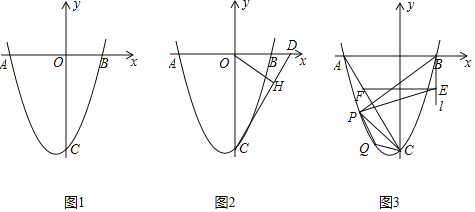
【題目】如圖1，拋物線
交x軸于點
，
，交y軸于點C．
求拋物線的解析式；
如圖2，D點坐標為
，連結
若點H是線段DC上的一個動點，求
的最小值．
如圖3，連結AC，過點B作x軸的垂線l，在第三象限中的拋物線上取點P，過點P作直線AC的垂線交直線l于點E，過點E作x軸的平行線交AC于點F，已知
．
求點P的坐標；
在拋物線上是否存在一點Q，使得
成立？若存在，求出Q點坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某民營企業準備用14000元從外地購進A、B兩種商品共600件，其中A種商品的成本價為20元，B種商品的成本價為30元．
(1)該民營企業從外地購得A、B兩種商品各多少件？
(2)該民營企業計劃租用甲、乙兩種貨車共6輛，一次性將A、B兩種商品運往某城市，已知每輛甲種貨車最多可裝A種商品110件和B種商品20件；每輛乙種貨車最多可裝A種商品30件和B種商品90件，問安排甲、乙兩種貨車有幾種方案？請你設計出具體的方案．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖,某塔觀光層的最外沿點E為蹦極項目的起跳點.已知點E離塔的中軸線AB的距離OE為10米,塔高AB為123米(AB垂直地面BC),在地面C處測得點E的仰角α=45°,從點C沿CB方向前行40米到達D點,在D處測得塔尖A的仰角β=60°,求點E離地面的高度EF.(結果精確到0.1米)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，從一架水平飛行的無人機
的尾端點
測得正前方的橋的左端點
俯角為
，且
，無人機的飛行高度
米，橋的長度
為1255米.
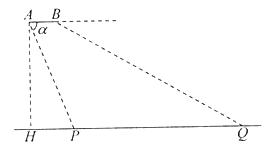
（1）求點
到橋左端點的距離；
（2）若從無人機前端點
測得正前方的橋的右端點
的俯角為
，求這架無人機的長度.
查看答案和解析>>
科目：初中數學 來源： 題型：
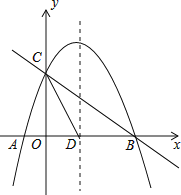
【題目】如圖，拋物線
與x軸交于A、B兩點，與y軸交于點C，拋物線的對稱軸交x軸于點D，已知
，
．
求拋物線的表達式；
在拋物線的對稱軸上是否存在點P，使
是以CD為腰的等腰三角形？如果存在，直接寫出P點的坐標；如果不存在，請說明理由；
點E是線段BC上的一個動點，過點E作x軸的垂線與拋物線相交于點F，當點E運動到什么位置時，四邊形CDBF的面積最大？求出四邊形CDBF的最大面積及此時E點的坐標．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
