【題目】形如：
的函數叫二次函數，它的圖象是一條拋物線．類比一元一次方程的解可以看成兩條直線的交點的橫坐標；則一元二次方程
的解可以看成拋物線
與直線
（
軸）的交點的橫坐標；也可以看成是拋物線
與直線
________的交點的橫坐標；也可以看成是拋物線________與直線
的交點的橫坐標；
新課標階梯閱讀訓練系列答案科目：初中數學 來源： 題型：
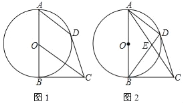
【題目】如圖1，AB是⊙O的直徑，BC是⊙O的切線，OC∥弦AD
（1）求證：CD是⊙O的切線；
（2）如圖2，連AC交BD于E．若AE=CE，求tan∠ACB的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，已知
是等邊三角形，邊
上有一點
，且
、
兩點之間的距離為
.
(1)求的坐標(用含有
的式子表示)；
(2)如圖(1)，若點
在線段
上運動，點
在
軸的正半軸上運動.當
的值最小時，
.
問：的面積是否為定值，若是，求其值；若不是，請說明理由.
(3)如圖(2)，若在外還有一點
，連接
、
、
、
，
，
，求的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，已知拋物線
過
，
，
三點，點的坐標是
，點的坐標是
，動點
在拋物線上．
________，
________，點的坐標為________；（直接填寫結果）
是否存在點，使得
是以
為直角邊的直角三角形？若存在，求出所有符合條件的點的坐標；若不存在，說明理由；
過動點作
垂直
軸于點
，交直線于點
，過點作
軸的垂線．垂足為
，連接
，當線段的長度最短時，求出點的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）先化簡，再求值：a（a-2b）+（a+b）2，其中a=-1，b=
;
（2）若x2-5x=3，求（x-1）（2x-1）-（x+1）2+1的值.
【答案】（1）原式= 2a2+b2=2+2=4；（2）原式=4.
【解析】試題分析：(1)利用完全平方公式展開，化簡，代入求值. (2) 利用完全平方公式展開，化簡，整體代入求值.
解：（1）原式=a2-2ab+a2+2ab+b2=2a2+b2.
當a=-1，b=
時，原式=2+2=4.
（2）原式=2x2-3x+1-（x2+2x+1）+1=x2-5x+1=3+1=4.
【題型】解答題
【結束】
22
【題目】已知化簡（x2+px+8）（x2-3x+q）的結果中不含x2項和x3項.
（1）求p，q的值.
（2）x2-2px+3q是否是完全平方式？如果是，請將其分解因式；如果不是，請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】百匯超市服裝柜在銷售中發現：“七彩”牌童裝平均每天可售出
件，每件盈利
元．為了迎接“元旦”，商場決定采取適降價措施，擴大銷售量，增加盈利，減少庫存．經市場調查發現：如果每件童裝降價
元，那么平均每天就可多售出
件．
如果每件降價
元，那么平均每天可售出幾件？
要想平均每天銷售這種童裝上盈利
元，那么每件童裝應降價多少元？
用配方法說明：要想盈利最多，每件童裝應降價多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知∠MON=20° ，點A B分別是射線OM、ON上的動點(A、B不與點0重合),若AB
OM，在射線ON上有一點C，設∠OAC=x°，下列x的值不能使△ABC為等腰三角形的是( )
A.20
B.45
C.50
D.125
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1, △ABC和△CDE均為等腰三角形，AC=BC, CD=CE, AC>CD, ∠ACB=∠DCE=a，且點A、D、E在同一直線上，連結BE.
(1)求證: AD=BE.
(2)如圖2,若a=90°，CM⊥AE于E.若CM=7, BE=10, 試求AB的長.
(3)如圖3,若a=120°, CM⊥AE于E, BN⊥AE于N, BN=a, CM=b,直接寫出AE的值(用a, b 的代數式表示).
查看答案和解析>>
科目：初中數學 來源： 題型：
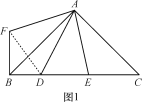
【題目】(1)如圖1，△ABC中，∠BAC＝90°，AB＝AC，D，E在BC上，∠DAE＝45°，為了探究BD，DE，CE之間的等量關系，現將△AEC繞A順時針旋轉90°后成△AFB，連接DF，經探究，你所得到的BD，DE，CE之間的等量關系式是 ；(無須證明)
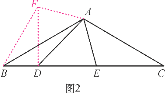
(2)如圖2，在△ABC中，∠BAC＝120°，AB＝AC，D，E在BC上，∠DAE＝60°，∠ADE＝45°，試仿照(1)的方法，利用圖形的旋轉變換，探究BD，DE，CE之間的等量關系，并證明你的結論．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
