
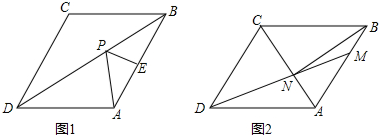
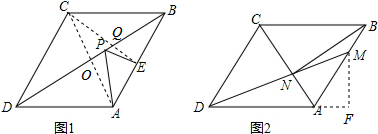
 (1)如圖1,連接AC,CE,分別交BD于點O,Q,
(1)如圖1,連接AC,CE,分別交BD于點O,Q,
 .
. ,AF=3,
,AF=3, ,
,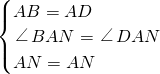 ,
,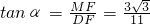 .
.

 小題狂做系列答案
小題狂做系列答案科目:初中數學 來源: 題型:
如圖是一個邊長為60cm的立方體ABCD—EFGH,一只甲蟲在菱EF上且距F點10cm的P處,它要爬到頂點D,需要爬行的最近距離是( )

A.130B.![]() C.
C.![]() D.不確定
D.不確定
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com