
【題目】如圖,在長方形ABCD中,DC=6cm,在DC上存在一點E,沿直線AE把三角形AE折疊,使點D恰好落在BC邊上,設此點為F,若三角形ABF的面積為24,那么CE長度為__________cm2.

【答案】![]()
【解析】
由折疊可得∠D=∠AFE=90°,結合已知條件不難證明△ABF∽△FCE,由三角形相似的性質可以得出EC與CF的比值,根據(jù)比值分別設出EC、CF的長度,進而表示出EF、DE的長度,列方程解出x,進而求出CE的長度.
∵矩形ABCD,
∴AB=CD=6cm,∠B=∠C=∠D=90°,
∵S△ABF=![]() AB·BF=
AB·BF=![]() ×6BF=24,
×6BF=24,
∴BF=8,
由折疊可得∠AFE=∠D=90°,DE=EF,
∴∠AFB+∠EFC=90°,
∵∠AFB+∠BAF=90°,
∴∠EFC=∠BAF,
∵在△ABF與△FCE中,
![]() ,
,
∴△ABF∽△FCE,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
設CE=4xcm,CF=3xcm,則EF=ED=5xcm,
∴6=5x+4x,
∴x=![]() ,
,
∴CE=![]() cm.
cm.
故答案為![]() .
.


科目:初中數(shù)學 來源: 題型:
【題目】李明從市場上買回一塊矩形鐵皮,他將此矩形鐵皮的四個角各剪去一個邊長為1米的正方形后,剩下的部分剛好能圍成一個容積為15立方米的無蓋長方體運輸箱,且此長方體運輸箱底面的長比寬多2米,現(xiàn)已知購買這種鐵皮每平方米需20元,問購買這張矩形鐵皮共花了多少錢?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】邊長為2的正方形OABC在平面直角坐標系中的位置如圖所示,點D是邊OA的中點,連接CD,點 E在第一象限,且DE⊥DC,DE=DC.以直線AB為對稱軸的拋物線過C,E兩點.
(1)求E點坐標;
(2)設拋物線的解析式為y=a(x﹣h)2+k,求a,h,k;
(3)點M為直線AB上一動點,點N為拋物線上一動點,是否存在點M,N,使得以點M,N,D,E為頂點的四邊形是平行四邊形?若存在,請直接寫出滿足條件的點M,N的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖所示,AE⊥AB,且AE=AB,BC⊥CD且BC=CD,若點E、B、D到直線AC的距離分別為6,3,4,則圖中實現(xiàn)所圍成的圖像面積是( )

A. 50 B. 44 C. 38 D. 32
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,△ABC的兩條角平分線BD、CE交于O,且∠A=60°,則下列結論中不正確的是( )
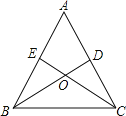
A.∠BOC=120° B.BC=BE+CD C.OD=OE D.OB=OC
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,二次函數(shù)y= ![]() x2(0≤x≤2)的圖象記為曲線C1 , 將C1繞坐標原點O逆時針旋轉90°,得曲線C2 .
x2(0≤x≤2)的圖象記為曲線C1 , 將C1繞坐標原點O逆時針旋轉90°,得曲線C2 . 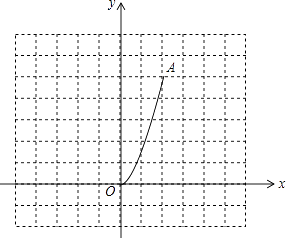
(1)請畫出C2;
(2)寫出旋轉后A(2,5)的對應點A1的坐標;
(3)直接寫出C1旋轉至C2過程中掃過的面積 .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】“國美”、“蘇寧”兩家電器商場出售同樣的空氣凈化器和過濾網(wǎng),空氣凈化器和過濾網(wǎng)在兩家商場的售價一樣.已知買一個空氣凈化器和![]() 個過濾網(wǎng)要花費
個過濾網(wǎng)要花費![]() 元,買
元,買![]() 個空氣凈化器和
個空氣凈化器和![]() 個過濾網(wǎng)要花費
個過濾網(wǎng)要花費![]() 元.
元.
(![]() )請用方程組求出一個空氣凈化器與一個過濾網(wǎng)的銷售價格分別是多少元?
)請用方程組求出一個空氣凈化器與一個過濾網(wǎng)的銷售價格分別是多少元?
(![]() )為了迎接新年,兩家商場都在搞促銷活動,“國美”規(guī)定:這兩種商品都打九五折;“蘇寧”規(guī)定:買一個空氣凈化器贈送兩個過濾網(wǎng).若某單位想要買
)為了迎接新年,兩家商場都在搞促銷活動,“國美”規(guī)定:這兩種商品都打九五折;“蘇寧”規(guī)定:買一個空氣凈化器贈送兩個過濾網(wǎng).若某單位想要買![]() 個空氣凈化器和
個空氣凈化器和![]() 個過濾網(wǎng),如果只能在一家商場購買,請問選擇哪家商場購買更合算?請說明理由.
個過濾網(wǎng),如果只能在一家商場購買,請問選擇哪家商場購買更合算?請說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com