
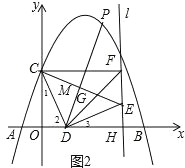
【題目】如圖,拋物線y=ax2+bx+3交x軸于A(﹣1,0)和B(5,0),交y軸于點C,點D是線段OB上一動點,連接CD,將CD繞點D順時針旋轉90°得到線段DE,過點E作直線l⊥x軸,垂足為H,過點C作CF⊥l于F,連接DF,CE交于點G.
(1)求拋物線解析式;
(2)求線段DF的長;
(3)當DG=![]() 時,
時,
①求tan∠CGD的值;
②試探究在x軸上方的拋物線上,是否存在點P,使∠EDP=45°?若存在,請寫出點P的坐標;若不存在,請說明理由.

【答案】(1)拋物線解析式為:y=﹣![]() x2+
x2+![]() x+3;(2)DF=
x+3;(2)DF=![]() =3
=3![]() ;(3)①tan∠CGD=3;
;(3)①tan∠CGD=3;
②P點坐標為(![]() ,
,![]() ).
).
【解析】
試題分析:(1)把A點和B點坐標代入y=ax2+bx+3中得到關于a、b的方程組,然后解方程組求出a、b即可得到拋物線解析式;
(2)如圖1,先求出C點坐標,再根據旋轉的性質得到CD=DE,∠CDE=90°,再證明△OCD≌△HDE得到HD=OC=3,接著說明四邊形OCFH為矩形得到HF=OC=3,然后利用勾股定理計算DF;
(3)①利用△CDE和△DFH都是等腰直角三角形得到∠DCE=45°,∠DFH=45°,于是有∠DFC=45°,則可證明△DCG∽△DFC,根據相似的性質得![]() =
=![]() ,∠DGC=∠DCF,接著利用相似比可計算出CD=
,∠DGC=∠DCF,接著利用相似比可計算出CD=![]() ,利用∠DCF=∠2得到∠CGD=∠2,然后在Rt△OCD中求出∠2的正切值即可得到tan∠CGD的值;
,利用∠DCF=∠2得到∠CGD=∠2,然后在Rt△OCD中求出∠2的正切值即可得到tan∠CGD的值;
②根據△DCG∽△DFC得到HD=OC=3,EH=OD=1,則E(4,1),取CE的中點M,如圖2,利用線段的中點坐標公式得到M(2,2),根據等腰直角三角形的性質判斷DP經過CE的中點M,接下來利用待定系數法求出直線DP的解析式為y=2x﹣2,然后解方程組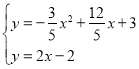 可得P點坐標.
可得P點坐標.
試題解析:(1)∵拋物線y=ax2+bx+3交x軸于A(﹣1,0)和B(5,0),
∴![]() ,解得
,解得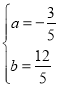 ,∴拋物線解析式為:y=﹣
,∴拋物線解析式為:y=﹣![]() x2+
x2+![]() x+3;
x+3;
(2)當x=0時,y=﹣![]() x2+
x2+![]() x+3=3,則C(0,3),如圖1,
x+3=3,則C(0,3),如圖1,
∵CD繞點D順時針旋轉90°得到線段DE,
∴CD=DE,∠CDE=90°,
∵∠2+∠3=90°,
而∠1+∠2=90°,
∴∠1=∠3,
在△OCD和△HDE中
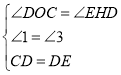 ,
,
∴△OCD≌△HDE,
∴HD=OC=3,
∵CF⊥BF,
∴四邊形OCFH為矩形,
∴HF=OC=3,
∴DF=![]() =3
=3![]() ;
;
(3)①∵△CDE和△DFH都是等腰直角三角形,如圖1,
∴∠DCE=45°,∠DFH=45°,
∴∠DFC=45°,
而∠CDG=∠FDC,
∴△DCG∽△DFC,
∴![]() ,∠DGC=∠DCF,即
,∠DGC=∠DCF,即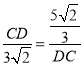 ,解得CD=
,解得CD=![]() ,
,
∵CF∥OH,
∴∠DCF=∠2,
∴∠CGD=∠2,
在Rt△OCD中,OD=![]() =
=![]() =1,
=1,
∴tan∠2=![]() =3,
=3,
∴tan∠CGD=3;
②∵OD=1,
∴D(1,0),
∵△OCD≌△HDE,
∴HD=OC=3,EH=OD=1,
∴E(4,1),
取CE的中點M,如圖2,則M(2,2),
∵△DCE為等腰直角三角形,∠EDP=45°,
∴DP經過CE的中點M,
設直線DP的解析式為y=mx+n,
把D(1,0),M(2,2)代入得![]() ,解得
,解得![]() ,
,
∴直線DP的解析式為y=2x﹣2,
解方程組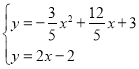 得
得 或
或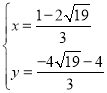 (舍去),
(舍去),
∴②P點坐標為(![]() ,
,![]() ).
).



 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案科目:初中數學 來源: 題型:
【題目】定義:圓心在三角形的一邊上,與另一邊相切,且經過三角形一個頂點(非切點)的圓,稱為這個三角形圓心所在邊上的“伴隨圓”.
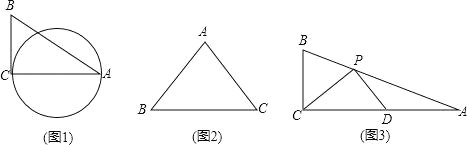
(1)如圖1,△ABC中,∠C=90°,AB=5,BC=3,則AC邊上的伴隨圓的半徑為 .
(2)如圖2,已知等腰△ABC,AB=AC=5,BC=6,畫草圖并直接寫出它的所有伴隨圓的半徑.
(3)如圖3,△ABC中,∠ACB=90°,點P在邊AB上,AP=2BP,D為AC中點,且∠CPD=90°.
①求證:△CPD的外接圓是△ABC某一條邊上的伴隨圓;
②求cos∠PDC的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】垃圾的分類處理與回收利用,可以減少污染,節省資源.某城市環保部門為了提高宣傳實效,抽樣調查了部分居民小區一段時間內生活垃圾的分類情況,其相關信息如圖:
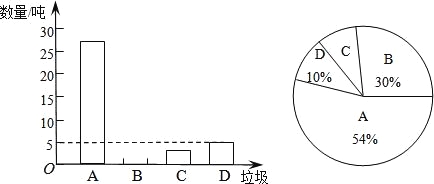
(注:A為可回收物,B為廚余垃圾,C為有害垃圾,D為其他垃圾)
根據圖表解答下列問題:
(1)在抽樣數據中,產生的有害垃圾共多少噸?
(2)請將條形統計圖補充完整;
(3)調查發現,在可回收物中塑料類垃圾占![]() ,每回收1噸塑料類垃圾可獲得0.7噸二級原料.假設該城市每月產生的生活垃圾為5000噸,且全部分類處理,那么每月回收的塑料類垃圾可以獲得多少噸二級原料?
,每回收1噸塑料類垃圾可獲得0.7噸二級原料.假設該城市每月產生的生活垃圾為5000噸,且全部分類處理,那么每月回收的塑料類垃圾可以獲得多少噸二級原料?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若a+b=2,則稱a與b是關于1的平衡數.
(1)3與 是關于1的平衡數,5﹣![]() 與 是關于1的平衡數;
與 是關于1的平衡數;
(2)若(m+![]() )×(1﹣
)×(1﹣![]() )=﹣5+3
)=﹣5+3![]() ,判斷m+
,判斷m+![]() 與5﹣
與5﹣![]() 是否是關于1的平衡數,并說明理由.
是否是關于1的平衡數,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,A(1,2),B(3,1),C(﹣2,﹣1).
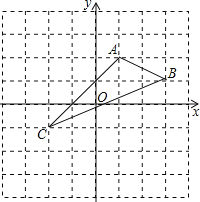
(1)在圖中作出△ABC關于y軸對稱的△A1B1C1.
(2)寫出A1,B1,C1的坐標(直接寫出答案),A1 ;B1 ;C1 .
(3)△ A1B1C1的面積為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】給出下列判斷:①在數軸上,原點兩旁的兩個點所表示的數都是互為相反數;②任何正數必定大于它的倒數;③5ab, ![]() ,
, ![]() 都是整式;④x2﹣xy+y2是按字母y的升冪排列的多項式,其中判斷正確的是( )
都是整式;④x2﹣xy+y2是按字母y的升冪排列的多項式,其中判斷正確的是( )
A.①②
B.②③
C.③④
D.①④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com