
【題目】如圖,已知:A、F、C、D四點在一條直線上,AF=CD,∠D=∠A,且AB=DE.請將下面說明△ABC≌△DEF的過程和理由補充完整.
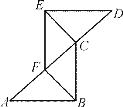
解:∵AF=CD(______)
∴AF+FC=CD+_____,即AC=DF,
在△ABC和△DEF中:AC=______(已知),∠D=∠A(________),AB=______(已知),
∴△ABC≌△DEF(_______)
科目:初中數學 來源: 題型:
【題目】(閱讀材科)小明同學發現這樣一個規律:兩個頂角相等的等腰三角形,
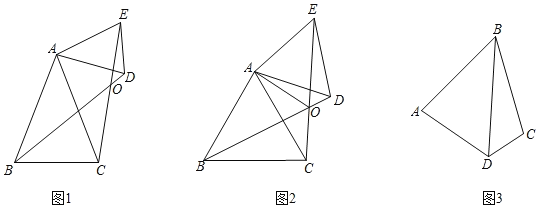
如果具有公共的項角的頂點,并把它們的底角頂點連接起來則形成一組全等的三角形,小明把具有這個規律的圖形稱為“手拉手”圖形.如圖1,在“手拉手”圖形中,小明發現若∠BAC=∠DAE,AB=AC,AD=AE,則△ABD≌△ACE.
(材料理解)(1)在圖1中證明小明的發現.
(深入探究)(2)如圖2,△ABC和△AED是等邊三角形,連接BD,EC交于點O,連接AO,下列結論:①BD=EC;②∠BOC=60°;③∠AOE=60°;④EO=CO,其中正確的有 .(將所有正確的序號填在橫線上).
(延伸應用)(3)如圖3,AB=BC,∠ABC=∠BDC=60°,試探究∠A與∠C的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,點A、B坐標分別為(4,2)、(0,2),線段CD在于x軸上,CD=![]() ,點C從原點出發沿x軸正方向以每秒1個單位長度向右平移,點D隨著點C同時同速同方向運動,過點D作x軸的垂線交線段AB于點E、交OA于點G,連結CE交OA于點F.設運動時間為t,當E點到達A點時,停止所有運動.
,點C從原點出發沿x軸正方向以每秒1個單位長度向右平移,點D隨著點C同時同速同方向運動,過點D作x軸的垂線交線段AB于點E、交OA于點G,連結CE交OA于點F.設運動時間為t,當E點到達A點時,停止所有運動.
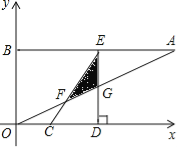
(1)求線段CE的長;
(2)記S為RtΔCDE與ΔABO的重疊部分面積,試寫出S關于t的函數關系式及t的取值范圍;
(3)連結DF,
①當t取何值時,有![]() ?
?
②直接寫出ΔCDF的外接圓與OA相切時t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 朗讀者
朗讀者![]() 自開播以來,以其厚重的文化底蘊和感人的人文情懷,感動了數以億計的觀眾,岳池縣某中學開展“朗讀”比賽活動,九年級
自開播以來,以其厚重的文化底蘊和感人的人文情懷,感動了數以億計的觀眾,岳池縣某中學開展“朗讀”比賽活動,九年級![]() 、
、![]() 班根據初賽成績,各選出5名選手參加復賽,兩個班各選出的5名選手的復賽成績
班根據初賽成績,各選出5名選手參加復賽,兩個班各選出的5名選手的復賽成績![]() 滿分為100分
滿分為100分![]() 如圖所示.
如圖所示.
平均數 | 中位數 | 眾數 | |
九 | 85 | 85 | |
九 | 80 |
![]() 根據圖示填寫表格;
根據圖示填寫表格;
![]() 結合兩班復賽成績的平均數和中位數,分析哪個班級的復賽成績較好;
結合兩班復賽成績的平均數和中位數,分析哪個班級的復賽成績較好;
![]() 如果規定成績較穩定班級勝出,你認為哪個班級能勝出?說明理由.
如果規定成績較穩定班級勝出,你認為哪個班級能勝出?說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在一面與地面垂直的圍墻的同側有一根高13米的旗桿AB和一根高度未知的電線桿CD,它們都與地面垂直,為了測得電線桿的高度,數學興趣小組的同學進行了如下測量![]() 某一時刻,在太陽光照射下,旗桿落在圍墻上的影子EF的長度為3米,落在地面上的影子BF的長為8米,而電線桿落在圍墻上的影子GH的長度為
某一時刻,在太陽光照射下,旗桿落在圍墻上的影子EF的長度為3米,落在地面上的影子BF的長為8米,而電線桿落在圍墻上的影子GH的長度為![]() 米,落在地面上的影子DH的長為6米,依據這些數據,該小組的同學計算出了電線桿的高度是______米
米,落在地面上的影子DH的長為6米,依據這些數據,該小組的同學計算出了電線桿的高度是______米![]()

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知⊙O的半徑為10,圓心O到弦AB的距離為5,則弦AB所對的圓周角的度數是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
查看答案和解析>>
科目:初中數學 來源: 題型:
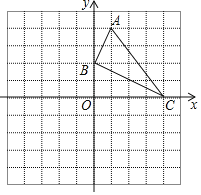
【題目】如圖,已知網格上最小的正方形的邊長為![]() (長度單位),點
(長度單位),點![]() 在格點上.
在格點上.
(1)直接在平面直角坐標系中作出![]() 關于
關于![]() 軸對稱的圖形
軸對稱的圖形![]() (點
(點![]() 對應點
對應點![]() ,點
,點![]() 對應點
對應點![]() );
);
(2)![]() 的面積為 (面積單位)(直接填空);
的面積為 (面積單位)(直接填空);
(3)點![]() 到直線
到直線![]() 的距離為 (長度單位)(直接填空);
的距離為 (長度單位)(直接填空);
查看答案和解析>>
科目:初中數學 來源: 題型:
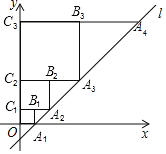
【題目】在平面直角坐標系xOy中,直線l:y=2x﹣2與x軸交于點A1,如圖所示,依次作正方形A1B1C1O,正方形A2B2C2C1,…,正方形AnBnnCn﹣1,使得點A1,A2,A3,…An在直線l上,點C1,C2,C3,…n在y軸正半軸上,則正方形AnBnnCn﹣1的面積是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】大家看過中央電視臺“購物街”節目嗎?其中有一個游戲環節是大轉輪比賽,轉輪上平均分布著5、10、15、20一直到100共20個數字.選手依次轉動轉輪,每個人最多有兩次機會.選手轉動的數字之和最大不超過100者為勝出;若超過100則成績無效,稱為“爆掉”.
(1)某選手第一次轉到了數字5,再轉第二次,則他兩次數字之和為100的可能性有多大?
(2)現在某選手第一次轉到了數字65,若再轉第二次了則有可能“爆掉”,請你分析“爆掉”的可能性有多大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com