
【題目】課上老師提出一個問題:“如圖,已知![]() ,
,![]() 于點
于點![]() ,
,![]() 交
交![]() 于點
于點![]() ,當
,當![]() 時,求
時,求![]() 的度數.”
的度數.”
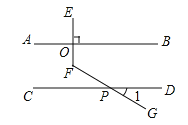
甲、乙、丙三位同學用不同的方法添加輔助線解決問題如圖1,圖2,圖3所示.
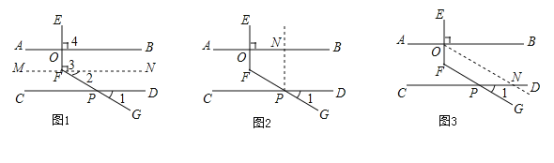
(1)補全甲同學的分析思路.
輔助線:過點![]() 作
作![]() .
.
分析思路:
①欲求∠EFG的度數,由圖可知只需轉化為求________和___________的度數之和;
②由輔助線作圖可知![]() ;
;
③由![]() ,
,![]() 推出_________________,由此可推出
推出_________________,由此可推出![]() ;
;
④由已知![]() ,可得
,可得![]() ,所以可得
,所以可得![]() 的度數,從而可求
的度數,從而可求![]() 的度數.
的度數.
(2)請你根據乙同學所畫的輔助線,補全求解過程.
解:過![]() 作___________________,交
作___________________,交![]() 于點
于點![]() .
.
![]() ___________________________
___________________________![]() (兩直線平行,同位角相等).
(兩直線平行,同位角相等).
![]() ,
,
![]() ,
,
![]() (_______________________).
(_______________________).
![]() .
.
![]() (____________________________),
(____________________________),
![]() ,
,
![]() _______________________.
_______________________.
(3)請你根據丙同學所畫的輔助線,求![]() 的度數.
的度數.
【答案】(1)∠2;∠3;AB∥MN;(2)NP∥EF;∠NPG;兩直線平行,同位角相等;兩直線平行,同旁內角互補;120°;(3)∠EFG=120°
【解析】
(1)根據已作輔助線及平行于同一條直線的兩條直線平行即可解答;
(2)根據垂線的定義以及平行線的性質即可解答;
(3)根據平行線的性質即可解答.
解:(1)∵∠EFG=∠2+∠3,
∴欲求∠EFG的度數,由圖可知只需轉化為求∠2和∠3的度數之和;
由![]() ,
,![]() 推出AB∥MN,
推出AB∥MN,
故答案為:∠2;∠3;AB∥MN.
(2)過![]() 作NP∥EF,交
作NP∥EF,交![]() 于點
于點![]() .
.
∴∠NPG![]() (兩直線平行,同位角相等).
(兩直線平行,同位角相等).
![]() ,
,
![]() ,
,
![]() (兩直線平行,同位角相等).
(兩直線平行,同位角相等).
![]() .
.
∴![]() (兩直線平行,同旁內角互補),
(兩直線平行,同旁內角互補),
![]() ,
,
![]() 120°.
120°.
故答案為:NP∥EF;∠NPG;兩直線平行,同位角相等;兩直線平行,同旁內角互補;120°
(3)如圖,過點O作ON∥FG,
∵ON∥FG,
∴∠EFG=∠EON,∠1=∠ONC=30°,
∵AB∥CD,
∴∠ONC=∠BON=30°,
∵EF⊥AB
∴∠EOB=90°,
∴∠EFG=∠EON=∠EOB+∠BON=90°+30°=120°.


 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業安徽少年兒童出版社系列答案
暑假作業安徽少年兒童出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知頂點為(﹣3,﹣6)的拋物線y=ax2+bx+c經過點(﹣1,﹣4),則下列結論中錯誤的是( )

A. b2>4ac
B. ax2+bx+c≥﹣6
C. 若點(﹣2,m),(﹣5,n)在拋物線上,則m>n
D. 關于x的一元二次方程ax2+bx+c=﹣4的兩根為﹣5和﹣1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)平面上有四個點A,B,C,D,按照以下要求作圖:
①作直線AD;
②作射線CB交直線AD于點E;
③連接AC,BD交于點F;
(2)圖中共有 條線段;
(3)若圖中F是AC的一個三等分點,AF<FC,已知線段AC上所有線段之和為18,求AF長.
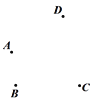
查看答案和解析>>
科目:初中數學 來源: 題型:
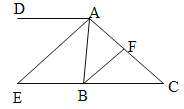
【題目】如圖,已知![]() .
.
(1)若![]() ,
,![]() 平分
平分![]() ,求
,求![]() 的度數;
的度數;
(2)若![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
①求證![]() ;
;
②將結論![]() 與條件
與條件![]() 互換位置,其他條件不變,組成一個新的命題,判斷該命題的真假,并寫出證明過程.
互換位置,其他條件不變,組成一個新的命題,判斷該命題的真假,并寫出證明過程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】推理探索:(1)數軸上點![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分別表示數0、 2 、3、5、 4 ,解答下列問題.
分別表示數0、 2 、3、5、 4 ,解答下列問題.
①畫出數軸表示出點![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ;
;
![]()
②![]() 、
、![]() 兩點之間的距離是 ;
兩點之間的距離是 ;
③![]() 、
、![]() 兩點之間的距離是 ;
兩點之間的距離是 ;
④![]() 、
、 ![]() 兩點之間的距離是 ;
兩點之間的距離是 ;
(2)請思考,若點![]() 表示數
表示數![]() 且
且![]() ,點
,點 ![]() 表示數
表示數![]() ,且
,且 ![]() ,則用含
,則用含 ![]() ,
,![]() 的代數式表示
的代數式表示 ![]() 、
、![]() 兩點 間的距離是 ;
兩點 間的距離是 ;
(3)請歸納,若點![]() 表示數
表示數![]() ,點
,點 ![]() 表示數
表示數![]() ,則
,則 ![]() 、
、![]() 兩點間的距離用含
兩點間的距離用含![]() 、
、![]() 的代數式表示是 .
的代數式表示是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB,AC分別是半⊙O的直徑和弦,OD⊥AC于點D,過點A作半⊙O的切線AP,AP與OD的延長線交于點P.連接PC并延長與AB的延長線交于點F.
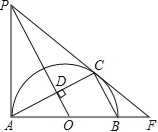
(1)求證:PC是半⊙O的切線;
(2)若∠CAB=30°,AB=10,求線段BF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程(m-1)x2-x-2=0.
(1)若x=-1是方程的一個根,求m的值和方程的另一根;
(2)當m為何實數時,方程有兩個不相等的實數根?
(3)若x1,x2是方程的兩個實數根,且xx2+x1x=-![]() ,試求實數m的值.
,試求實數m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知在△ABC中,∠ABC與∠ACB的平分線交于點P.
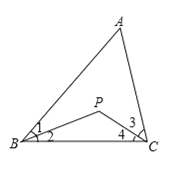
(1)當∠A=40°,∠ABC=60°時,求∠BPC的度數;
(2)當∠A=α°時,求∠BPC的度數.(用α的代數式表示)
(3)小明研究時發現:如果延長AB至D,再過點B作BQ⊥BP,那么BQ就是∠CBD的平分線。請你證明小明的結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com