
【題目】在互聯網技術的影響下,幸福新村的村民小劉在網上銷售蘋果,原計劃每天賣100千克,但實際每天的銷量與計劃銷量相比有出入,如表是某周的銷售情況(超額記為正,不足記為負.單位:千克):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
與計劃量的差值 |
|
|
|
|
|
|
|
(1)根據表中的數據可知前三天共賣出___________千克;
(2)根據記錄的數據可知銷售量最多的一天比銷售量最少的一天多銷售多少千克?
(3)若每千克按5元出售,每千克蘋果的運費為1元,那么小劉本周一共收入多少元?
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,BC=2AB,對角線相交于O,過C點作CE⊥BD交BD于E點,H為BC中點,連接AH交BD于G點,交EC的延長線于F點,下列5個結論:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四邊形GHCE;⑤CF=BD.正確的有( )個.
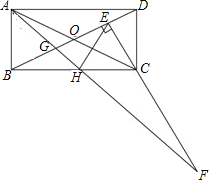
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料:如圖1,圓的概念:在平面內,線段PA繞它固定的一個端點P旋轉一周,另一個端點A所形成的圖形叫做圓.就是說,到某個定點等于定長的所有點在同一個圓上.圓心在P(a,b),半徑為r的圓的方程可以寫為:(x-a)2+(y-b)2=r2.如:圓心在P(2,-1),半徑為5的圓的方程為:(x-2)2+(y+1)2=25.
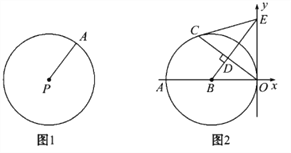
(1)填空: ①以A(3,0)為圓心,1為半徑的圓的方程為:________; ②以B(-1,-2)為圓心, ![]() 為半徑的圓的方程為:________;
為半徑的圓的方程為:________;
(2)根據以上材料解決以下問題:
如圖2,以B(-6,0)為圓心的圓與y軸相切于原點,C是☉B上一點,連接OC,作BD⊥OC垂足為D,延長BD交y軸于點E,已知sin∠AOC=![]() .
.
①連接EC,證明EC是☉B的切線;
②在BE上是否存在一點P,使PB=PC=PE=PO,若存在,求P點坐標,并寫出以P為圓心,以PB為半徑的☉P的方程;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知A、B兩個蔬菜市場各有蔬菜14噸,現要全部運往甲、乙兩地,其中甲地需要蔬菜15噸,乙地需要蔬菜13噸,從蔬菜市場A到甲地運費50元/噸,到乙地30元/噸;從蔬菜市場B到甲地運費60元/噸,到乙地45元/噸。
(1)設從蔬菜市場A向甲地運送蔬菜x噸,請完成下表:
運往甲地(單位:噸) | 運往乙地(單位:噸) | |
蔬菜市場A | x | |
蔬菜市場B |
(2)若總運費為1300元,則從蔬菜市場A向甲地運送蔬菜多少噸?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在△ABC中,D是BC邊上一點,E是AD的中點,過點A作BC的平行線交CE的延長線于F,且AF=BD,連接BF.
(1)求證:點D是線段BC的中點;
(2)如圖2,若AB=AC=13,AF=BD=5,求四邊形AFBD的面積.
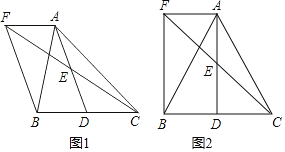
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知多項式(2x2+ax﹣y+6)﹣(2bx2﹣3x+5y﹣1).
(1)若多項式的值與字母x的取值無關,求a、b的值.
(2)在(1)的條件下,先化簡多項式3(a2﹣ab+b2)﹣(3a2+ab+b2),再求它的值.
(3)在(1)的條件下,求(b+a2)+(2b+![]() a2)+(3b+
a2)+(3b+![]() a2)+…+(9b+
a2)+…+(9b+![]() a2)的值.
a2)的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有依次3個數:2、9、7.對任意相鄰的兩個數,都用右邊的數減去左邊的數,所得之差寫在這兩個數之間,可產生一個新數串:2、7、9、-2、7,這稱為第1次操作,做第2次同樣的操作后也可以產生一個新數串:2、5、7、2、9、-11、-2、9、7,繼續(xù)依次操作下去,問從數串2、9、7開始操作第20次后所產生的那個數串的所有數之和是___________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣![]() +bx+c過點A(3,0),B(0,2).M(m,0)為線段OA上一個動點(點M與點A不重合),過點M作垂直于x軸的直線與直線AB和拋物線分別交于點P、N.
+bx+c過點A(3,0),B(0,2).M(m,0)為線段OA上一個動點(點M與點A不重合),過點M作垂直于x軸的直線與直線AB和拋物線分別交于點P、N.
(1)求直線AB的解析式和拋物線的解析式;
(2)如果點P是MN的中點,那么求此時點N的坐標;
(3)如果以B,P,N為頂點的三角形與△APM相似,求點M的坐標.
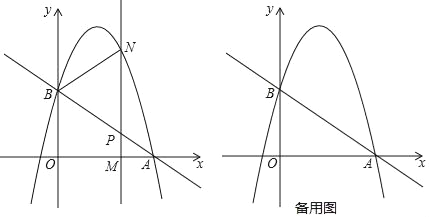
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們已經學習過反比例函數y=![]() 的圖像和性質,請你回顧研究它的過程,運用所學知識對函數y=
的圖像和性質,請你回顧研究它的過程,運用所學知識對函數y=![]() 的圖像和性質進行探索,并解決下列問題:
的圖像和性質進行探索,并解決下列問題:
(1)該函數的圖像大致是( )
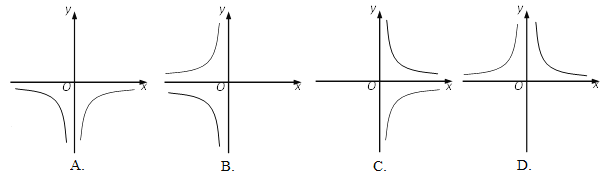
(2)寫出該函數兩條不同類型的性質:
① ;
② .
(3)寫出不等式![]() -3>0的解集.
-3>0的解集.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com