
【題目】問題提出
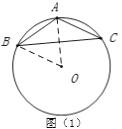
(1)如圖①,在△ABC中,∠A=120°,AB=AC=5,則△ABC的外接圓半徑R的值為 .
問題探究
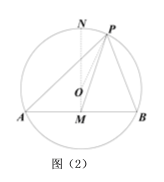
(2)如圖②,⊙O的半徑為13,弦AB=24,M是AB的中點,P是⊙O上一動點,求PM的最大值.
問題解決
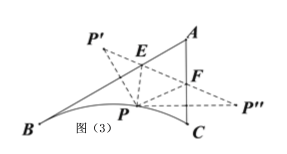
(3)如圖③所示,AB、AC、BC是某新區的三條規劃路其中,AB=6km,AC=3km,∠BAC=60°,BC所對的圓心角為60°.新區管委會想在BC路邊建物資總站點P,在AB、AC路邊分別建物資分站點E、F.也就是,分別在![]() 、線段AB和AC上選取點P、E、F.由于總站工作人員每天要將物資在各物資站點間按P→E→F→P的路徑進行運輸,因此,要在各物資站點之間規劃道路PE、EF和FP.為了快捷環保和節約成本要使得線段PE、EF、FP之和最短,試求PE+EF+FP的最小值(各物資站點與所在道路之間的距離、路寬均忽略不計).
、線段AB和AC上選取點P、E、F.由于總站工作人員每天要將物資在各物資站點間按P→E→F→P的路徑進行運輸,因此,要在各物資站點之間規劃道路PE、EF和FP.為了快捷環保和節約成本要使得線段PE、EF、FP之和最短,試求PE+EF+FP的最小值(各物資站點與所在道路之間的距離、路寬均忽略不計).



圖① 圖② 圖③
【答案】(1)5;(2)18;(3)(3![]() -9)km.
-9)km.
【解析】(1)如圖(1),設外接圓的圓心為O,連接OA, OB,根據已知條件可得△AOB是等邊三角形,由此即可得半徑;
(2)如圖(2)所示,連接MO并延長交⊙O于N,連接OP,顯然,MN即為MP的最大值,根據垂徑定理求得OM的長即可求得MN的最大值;
(3) 如圖(3)所示,假設P點即為所求點,分別作出點P關于AB、AC的對稱點P、P"連接PP、PE,PE,P"F,PF,PP",則PP"即為最短距離,其長度取決于PA的長度, 根據題意正確畫出圖形,得到點P的位置,根據等邊三角形、勾股定理等進行求解即可得PE+EF+FP的最小值.
(1)如圖(1),設外接圓的圓心為O,連接OA, OB,
∵O是等腰三角形ABC的外心,AB=AC,
∴∠BAO=∠OAC=![]() ∠BAC=
∠BAC=![]() =60°,
=60°,
∵OA=OB,
∴△AOB是等邊三角形,
∴OB=AB=5,
故答案為:5;
(2)如圖(2)所示,連接MO并延長交⊙O于N,連接OP,
顯然,MP≤OM+OP=OM+ON=MN,ON=13,OM=![]() =5,MN=18,
=5,MN=18,
∴PM的最大值為18;
(3) 如圖(3)所示,假設P點即為所求點,分別作出點P關于AB、AC的對稱點P、P"連接PP、PE,PE,P"F,PF,PP"
由對稱性可知PE+EF+FP=PE+EF+FP"=PP",且P、E、F、P"在一條直線上,所以PP"即為最短距離,其長度取決于PA的長度,
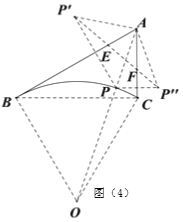
如圖(4),作出弧BC的圓心O,連接AO,與弧BC交于P,P點即為使得PA最短的點,∵AB=6km,AC=3km,∠BAC=60°,
∴ABC是直角三角形,∠ABC=30°,BC=3![]() ,
,
BC所對的圓心角為60°,∴OBC是等邊三角形,∠CBO=60°,BO=BC=3![]() ,
,
∴∠ABO=90°,AO=3![]() ,PA=3
,PA=3![]() -3
-3![]() ,
,
∠PAE=∠EAP,∠PAF=∠FAP",
∴∠PAP"=2∠ABC=120°,PA=AP",
∴∠APE=∠AP"F=30°,
∵PP"=2PAcos∠APE=![]() PA=3
PA=3![]() -9,
-9,
所以PE+EF+FP的最小值為3![]() -9km.
-9km.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】為了推動我縣“三進校園”活動的廣泛開展,引導學生走向操場,走到陽光下,積極參加體育鍛煉,學校準備購買一批運動鞋供學生借用,現從各年級隨機抽取了部分學生的鞋號,繪制了如下的統計圖①和圖②,請根據相關信息,解答下列問題:

(1)本次接受隨機抽樣調查的學生人數為 ,圖①中![]() 的值為 ;
的值為 ;
(2)本次調查獲取的樣本數據的眾數為 ,中位數為 ;
(3)根據樣本數據,若學校計劃購買![]() 雙運動鞋,建議購買
雙運動鞋,建議購買![]() 號運動鞋 雙.
號運動鞋 雙.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=13,BC=14,AC=15,點D在AC上(可與點A,C重合),分別過點A、C作直線BD的垂線,垂足為E,F,則AE+CF的最大值為_____,最小值為_____.
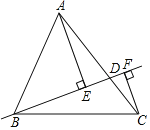
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某人去年水果批發市場采購蘋果,他看中了![]() 、
、![]() 兩家蘋果.這兩家蘋果品質一樣,零售價都為6元/千克,批發價各不相同.
兩家蘋果.這兩家蘋果品質一樣,零售價都為6元/千克,批發價各不相同.
(1)![]() 家規定:批發數量不超過1000千克,按零售價的92%優惠;批發數量超過1000千克且不超過2000千克,所有蘋果按零售價的90%優惠;超過2000千克,所有蘋果按零售價的88%優惠.
家規定:批發數量不超過1000千克,按零售價的92%優惠;批發數量超過1000千克且不超過2000千克,所有蘋果按零售價的90%優惠;超過2000千克,所有蘋果按零售價的88%優惠.
![]() 家的規定如下表:
家的規定如下表:
數量范圍(千克) | 0—500 | 500以上—1500 | 1500以上—2500 | 2500以上 |
價格(元) | 零售價的95% | 零售價的85% | 零售價的75% | 零售價的70% |
表格說明:批發價格分段計算,如某人批發蘋果2100千克,則總費用=6×95%×500+6×85%×1000+6×75%×(2100-1500).
(1)如果他批發600千克蘋果,那么他在![]() 、
、![]() 兩家批發分別需要多少元?
兩家批發分別需要多少元?
(2)如果他批發![]() 千克蘋果(1500<
千克蘋果(1500<![]() <2000),請你分別用含
<2000),請你分別用含![]() 的代數式表示在
的代數式表示在![]() 、
、![]() 兩家批發所需的費用.
兩家批發所需的費用.
(3)現在他要批發1800千克蘋果,選擇在哪家批發更優惠呢?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知等邊三角形ABC的頂點B、C的坐標分別為(0,0)和(0,4).
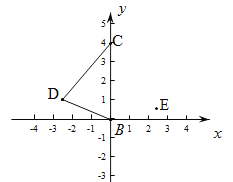
(1)求頂點A的坐標.
(2)D為第二象限內一點,作出點P,使得P到DB和DC的距離相等,且到點E的距離等于DB(不寫作法,保留作圖痕跡).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,點P在對角線AC上,且PA=PD,⊙O是△PAD的外接圓.
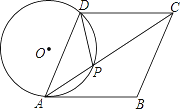
(1)求證:AB是⊙O的切線;
(2)若AC=8,tan∠BAC=![]() ,求⊙O的半徑.
,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近年來,隨著新能源汽車推廣力度加大,產業快速發展,越來越多的消費者開始接受并購買新能源汽車,我國新能源汽車的生產量和銷售量都大幅增長,下圖是2014-2017年新能源汽車生產和銷售的情況:根據統計圖中提供的信息,預估全國2018年新能源汽車銷售量約為__________萬量,你的預估理由是____________________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某汽車銷售公司經銷某品牌A款汽車,隨著汽車的普及,其價格也在不斷下降.今年5月份A款汽車的售價比去年同期每輛降價1萬元,如果賣出相同數量的A款汽車,去年銷售額為100萬元,今年銷售額只有90萬元.
(1)今年5月份A款汽車每輛售價多少萬元?
(2)為了增加收入,汽車銷售公司決定再經銷同品牌的B款汽車,已知A款汽車每輛進價為7.5萬元,B款汽車每輛進價為6萬元,公司預計用不多于105萬元且不少于99萬元的資金購進這兩款汽車共15輛,有幾種進貨方案?
(3)如果B款汽車每輛售價為8萬元,為打開B款汽車的銷路,公司決定每售出一輛B款汽車,返還顧客現金a萬元,要使(2)中所有的方案獲利相同,a值應是多少?此時,哪種方案對公司更有利?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com