
【題目】如圖,已知![]() ,
, ![]() ,
, ![]() ,試說明:BE∥CF.
,試說明:BE∥CF.
完善下面的解答過程,并填寫理由或數學式:
解:∵ ![]() (已知)
(已知)
∴AE∥ ( )
∴![]() ( )
( )
∵![]() (已知)
(已知)
∴![]() ( )
( )
∴DC∥AB( )
∴![]() ( )
( )
即![]()
∵![]() (已知)
(已知)
∴![]() ( )
( )
即![]()
∴BE∥CF( ) .

科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,菱形ABCD的頂點A在y軸上,且點A坐標為(0,4),BC在x軸正半軸上,點C在B點右側,反比例函數![]() (x>0)的圖象分別交邊AD,CD于E,F,連結BF,已知,BC=k,AE=
(x>0)的圖象分別交邊AD,CD于E,F,連結BF,已知,BC=k,AE=![]() CF,且S四邊形ABFD=20,則k= _________.
CF,且S四邊形ABFD=20,則k= _________.
[Failed to download image : http://192.168.0.10:8086/QBM/2019/1/17/2120855162306560/2123559773659136/STEM/85e8312ee4314e6b84d61ad733d78d14.png]
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,矩形OABC在平面直角坐標系內的位置如圖所示,點O為坐標原點,點A的坐標示為(10,0),點B的坐標為(10,8) .
(1)直接寫出點C的坐標為:C( ____ ,_____);
(2)已知直線AC與雙曲線y=![]() (m≠0)在第一象限內有一點交點Q為(5,n),
(m≠0)在第一象限內有一點交點Q為(5,n),
①求m及n的值;
②若動點P從A點出發,沿折線AO→OC→CB的路徑以每秒2個單位長度的速度運動,到達B處停止,△APQ的面積為S,當t取何值時,S=10.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在四邊形ABCD中,∠ABC=90°,∠CAB=∠CAD=22.5°,E在AB上,且∠DCE=67.5°,DE⊥AB于E,若AE=1,線段BE的長為____________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某旅客攜帶x kg的行李乘飛機,登機前,旅客可選擇托運或快遞行李,托運費y1(元)與行李重量x kg的對應關系由如圖所示的一次函數圖象確定,下表列出了快遞費y2(元)與行李重量x kg的對應關系


(1) 如果旅客選擇托運,求可攜帶的免費行李的最大重量為多少kg?
(2) 如果旅客選擇快遞,當1<x≤15時,直接寫出快遞費y2(元)與行李的重量x kg之間的函數關系式
(3) 某旅客攜帶25kg的行李,設托運m kg行李(10≤m<24,m為正整數),剩下的行李選擇快遞.當m為何值時,總費用y的值最小?并求出其最小值是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,若CO⊥AB,垂足為O,OE、OF分別平分∠AOC與∠BOC.求∠EOF的度數;
(2)如圖2,若∠AOC=∠BOD=80°,OE、OF分別平分∠AOD與∠BOC.求∠EOF的度數;
(3)若∠AOC=∠BOD=α,將∠BOD繞點O旋轉,使得射線OC與射線OD的夾角為β,OE、OF分別平分∠AOD與∠BOC.若α+β≤180°,α>β,則∠EOC= .(用含α與β的代數式表示)

查看答案和解析>>
科目:初中數學 來源: 題型:
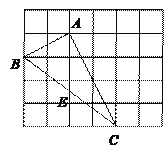
【題目】如圖,在邊長為1的小正方形組成的網格中,△ABC的三個頂點均在格點上,請按要求完成下列各題:
(1)畫線段AD∥BC且使AD=BC,連接CD;
(2)線段AC的長為_______,CD的長為______,AD的長為________;
(3)四邊形ABCD的面積為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
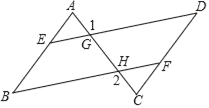
【題目】在括號內注明說理依據.如圖已知∠B=∠D,∠1=∠2,試猜想∠A與∠C的大小關系,并說明理由.
解:猜想∠A=∠C
∵∠1=∠2 (已知)
∠1=∠EGC
∴∠2=∠EGC
∴BF∥DE
∴∠B=∠AED
∵∠B=∠D
∴∠AED=∠D (等量代換)
∴AB∥CD
∴∠A=∠C .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com