
 ×4×5=20,
×4×5=20, ×100×101×102=343400;
×100×101×102=343400; (1×2×3﹣0×1×2),
(1×2×3﹣0×1×2), (2×3×4﹣1×2×3),
(2×3×4﹣1×2×3), (3×4×5﹣2×3×4),
(3×4×5﹣2×3×4), [n(n+1)(n+2)﹣(n﹣1)n(n+1)],
[n(n+1)(n+2)﹣(n﹣1)n(n+1)], [1×2×3﹣0×1×2+2×3×4﹣1×2×3+3×4×5﹣2×3×4+…+n(n+1)(n+2)﹣(n﹣1)n(n+1)],
[1×2×3﹣0×1×2+2×3×4﹣1×2×3+3×4×5﹣2×3×4+…+n(n+1)(n+2)﹣(n﹣1)n(n+1)], n(n+1)(n+2);
n(n+1)(n+2); (1×2×3×4﹣0×1×2×3),
(1×2×3×4﹣0×1×2×3), (2×3×4×5﹣1×2×3×4),
(2×3×4×5﹣1×2×3×4), [n(n+1)(n+2)(n+3)﹣(n﹣1)n(n+1)(n+2)],
[n(n+1)(n+2)(n+3)﹣(n﹣1)n(n+1)(n+2)], (1×2×3×4﹣0×1×2×3+2×3×4×5﹣1×2×3×4+…+n(n+1)(n+2)(n+3)﹣(n﹣1)n(n+1)(n+2)],
(1×2×3×4﹣0×1×2×3+2×3×4×5﹣1×2×3×4+…+n(n+1)(n+2)(n+3)﹣(n﹣1)n(n+1)(n+2)], n(n+1)(n+2)(n+3).
n(n+1)(n+2)(n+3). n(n+1)(n+2);(3)
n(n+1)(n+2);(3) n(n+1)(n+2)(n+3).
n(n+1)(n+2)(n+3).

科目:初中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
| 1 |
| 2 |
查看答案和解析>>
科目:初中數學 來源:湖北省期中題 題型:解答題
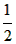 n(n+1),其中n為正整數,現在我們來研究一個類似的問題:1×2+2×3+…+n(n+1)=?
n(n+1),其中n為正整數,現在我們來研究一個類似的問題:1×2+2×3+…+n(n+1)=?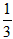 (1×2×3-0×1×2)
(1×2×3-0×1×2)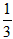 (2×3×4-1×2×3)
(2×3×4-1×2×3)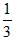 (3×4×5-2×3×4)
(3×4×5-2×3×4)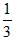 ×3×4×5=20;
×3×4×5=20;查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
閱讀材料,數學家高斯在上學時曾經研究過這樣一個問題,1+2+3+…+10=?
經過研究,這個問題的一般性結論是1+2+3+…+n=![]() n(n+1),其中n為正整數,現在我們來研究一個類似的問題:1×2+2×3+…+ n(n+1)=?
n(n+1),其中n為正整數,現在我們來研究一個類似的問題:1×2+2×3+…+ n(n+1)=?
觀察下面三個特殊的等式:
1×2=![]() (1×2×3-0×1×2)
(1×2×3-0×1×2)
2×3=![]() (2×3×4-1×2×3)
(2×3×4-1×2×3)
3×4=![]() (3×4×5-2×3×4)
(3×4×5-2×3×4)
將這三個等式的倆邊相加,可以得到1×2+2×3+3×4=![]() ×3×4×5=20.
×3×4×5=20.
讀完這段材料,請你計算:
(1)1×2+2×3+…+100×101;(只需寫出結果)(2分)
(2)1×2+2×3+…+ n(n+1);(寫出計算過程) (5分)
(3)1×2×3+2×3×4+…+ n(n+1)(n+2).(只需寫出結果)(3分)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com