
【題目】下面是小東設計的“作![]() 中
中![]() 邊上的高線”的尺規作圖過程.
邊上的高線”的尺規作圖過程.
已知:![]() .
.
求作:![]() 中
中![]() 邊上的高線
邊上的高線![]() .
.
作法:如圖,
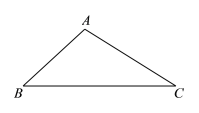
①以點![]() 為圓心,
為圓心,![]() 的長為半徑作弧,以點
的長為半徑作弧,以點![]() 為圓心,
為圓心,![]() 的長為半徑作弧,兩弧在
的長為半徑作弧,兩弧在![]() 下方交于點
下方交于點![]() ;
;
②連接![]() 交
交![]() 于點
于點![]() .
.
所以線段![]() 是
是![]() 中
中![]() 邊上的高線.
邊上的高線.
根據小東設計的尺規作圖過程,
(1)使用直尺和圓規,補全圖形;(保留作圖痕跡)
(2)完成下面的證明.
證明:∵ ![]() ,
, ![]() ,
,
∴點![]() ,
,![]() 分別在線段
分別在線段![]() 的垂直平分線上( )(填推理的依據).
的垂直平分線上( )(填推理的依據).
∴![]() 垂直平分線段
垂直平分線段![]() .
.
∴線段![]() 是
是![]() 中
中![]() 邊上的高線.
邊上的高線.
科目:初中數學 來源: 題型:
【題目】如圖①是一個長為2m.寬為2n的長方形,沿圖中虛線用剪刀均勻分成四塊小長方形,然后按圖②形狀拼成一個正方形.
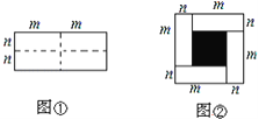
(1)你認為圖②中的陰影部分的正方形的邊長等于________?
(2)請用兩種不同的方法求圖②中陰影部分的面積.(不用化簡)
方法1:___________;方法2:___________.
(3)由問題(2)你能寫出三個代數式:![]() ,
,![]() ,mn之間的一個等量關系.
,mn之間的一個等量關系.
答:______________.
(4)根據(3)題中的等量關系和完全平方公式,解決如下問題:
①已知:m+n=5,mn=-3,求:(m﹣n)2的值;
②已知m-n=5,![]() ,求mn的值.
,求mn的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖示,若△ABC內一點P滿足∠PAC=∠PBA=∠PCB,則點P為△ABC的布洛卡點.三角形的布洛卡點(Brocard point)是法國數學家和數學教育家克洛爾(A.L.Crelle 1780﹣1855)于1816年首次發現,但他的發現并未被當時的人們所注意,1875年,布洛卡點被一個數學愛好者法國軍官布洛卡(Brocard 1845﹣1922)重新發現,并用他的名字命名.問題:已知在等腰直角三角形DEF中,∠EDF=90°,若點Q為△DEF的布洛卡點,DQ=1,則EQ+FQ=( ) 
A.5
B.4
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若點![]() ,
,![]() 在數軸上對應的數為
在數軸上對應的數為![]() ,
,![]() ,則稱
,則稱![]() 為點
為點![]() 和
和![]() 之間的距離,記作
之間的距離,記作![]() .已知數軸上兩點
.已知數軸上兩點![]() ,
,![]() 對應的數分別為
對應的數分別為![]() 和
和![]() ,且滿足
,且滿足![]() ,點
,點![]() 為數軸上一動點,其對應的數為
為數軸上一動點,其對應的數為![]() .
.
(1)若點![]() 到點
到點![]() 和
和![]() 的距離相等,則點
的距離相等,則點![]() 對應的數是_________.
對應的數是_________.
(2)數軸上是否存在點![]() ,使
,使![]() ?若存在,請求出
?若存在,請求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
(3)當點![]() 以每秒1個單位長度的速度從原點向左運動時,點
以每秒1個單位長度的速度從原點向左運動時,點![]() 以每秒3個單位長度向左運動,點
以每秒3個單位長度向左運動,點![]() 以每秒15個單位長度向左運動,若它們同時出發,幾秒鐘后點
以每秒15個單位長度向左運動,若它們同時出發,幾秒鐘后點![]() 到點
到點![]() 和
和![]() 的距離相等?
的距離相等?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某開發公司生產的 960 件新產品需要精加工后,才能投放市場,現甲、乙兩個工廠都想加工這批產品,已知甲工廠單獨加工完成這批產品比乙工廠單獨加工完成這批產品多用 20 天,而甲工廠每天加工的數量是乙工廠每天加工的數量的![]() ,公司需付甲工廠加工費用為每天 80 元,乙工廠加工費用為每天 120 元.
,公司需付甲工廠加工費用為每天 80 元,乙工廠加工費用為每天 120 元.
(1)甲、乙兩個工廠每天各能加工多少件新產品?
(2)公司制定產品加工方案如下:可以由每個廠家單獨完成,也可以由兩個廠家合作完成.在加工過程中,公司派一名工程師每天到廠進行技術指導,并負擔每天 15 元的午餐補助費, 請你幫公司選擇一種既省時又省錢的加工方案,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中, A、B兩點分別在x軸、y軸的正半軸上,且OB = OA=3.(1)、求點A、B的坐標;(2)、已知點C(-2,2),求△BOC的面積;(3)、點P是第一象限角平分線上一點,若![]() ,求點P的坐標.
,求點P的坐標.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com