【題目】某工廠現有甲種原料360千克，乙種原料290千克，計劃利用這兩種原料生產A、B兩種產品50件．生產一件A產品需要甲種原料9千克，乙種原料3千克，可獲利潤700元；生產一件B產品，需要甲種原料4千克，乙種原料10千克，可獲利潤1200元．
（1）設生產x件A種產品，寫出其題意x應滿足的不等式組；
（2）由題意有哪幾種按要求安排A、B兩種產品的生產件數的生產方案？請您幫助設計出來．
【答案】（1）
；（2）有3種生產方案：方案1：A產品30件，B產品20件；方案2：A產品31件，B產品19件；方案3：A產品32件，B產品18件．
【解析】分析：（1）設生產x件A種產品，則生產B產品（50﹣x）件，共需要甲種原料[9x+4（50﹣x）]千克，乙種原料[3x+10（50﹣x）]千克，根據題意就可以建立不等式組；
（2）求出（1）的不等式組的解集，就可以確定x的值，從而求出生產方案．
詳解：（1）設生產x件A種產品，則生產B產品（50﹣x）件，共需要甲種原料[9x+4（50﹣x）]千克，乙種原料[3x+10（50﹣x）]千克，由題意得：
；
（2）∵，解得：30≤x≤32，∴x為整數，∴x=30，31，32，∴有3種生產方案：
方案1：A產品30件，B產品20件；
方案2：A產品31件，B產品19件；
方案3：A產品32件，B產品18件．
習題精選系列答案科目：初中數學 來源： 題型：
【題目】如圖，已知反比例函數y= 
（x＞0）的圖象與一次函 數y=﹣x+b的圖象分別交于A（1，3）、B兩點．
（1）求m、b的值；
（2）若點M是反比例函數圖象上的一動點，直線MC⊥x軸于C，交直線AB于點N，MD⊥y軸于D，NE⊥y軸于E，設四邊形MDOC、NEOC的面積分別為S1、S2 ， S=S2﹣S1 ， 求S的最大值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AD平分∠BAC交BC于點D，點F在BA的延長線上，點E在線段CD上，EF與AC相交于點G，∠BDA+∠CEG=180°．
（1）AD與EF平行嗎？請說明理由；
（2）若點H在FE的延長線上，且∠EDH=∠C，則∠F與∠H相等嗎，請說明理由．
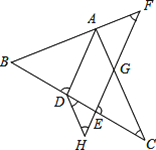
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB=AC，BD平分∠ABC交AC于點D，AE∥BD交CB的延長線于點E．若∠E=35°，則∠BAC的度數為（ ）
A. 40° B. 45° C. 60° D. 70°
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】按照題中提供的思路點撥，先填空，然后完成解答的全過程.
如圖，已知AB＝AD，∠BAD＝60°，∠BCD＝120°，延長BC，使CE＝CD，連接DE，求證：BC+DC＝AC.
思路點撥：（1）由已知條件AB＝AD，∠BAD＝60°，可知△ABD是＿三角形.同理由已知條件∠BCD＝120°得到∠DCE＝＿，且CE＝CD，可知＿；
（2）要證BC+DC＝AC，可將問題轉化為證兩條線段相等，即＿＝＿；
（3）要證（2）中所填寫的兩條線段相等，可以先證明＿.請寫出完整的證明過程.
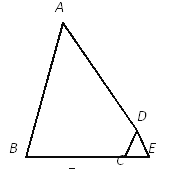
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某高校共有5個大餐廳和2個小餐廳。經過測試：同時開放1個大餐廳和2個小餐廳，可供1680名學生就餐；同時開放2個大餐廳和1個小餐廳，可供2280名學生就餐。
（1）1個大餐廳和1個小餐廳分別可供多少名學生就餐？
（2）若7個餐廳同時開放，能否供全校的5300名學生就餐？請說明理由
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】體育委員統計了全班同學60秒跳繩的次數，并列出下列人數次數分布表，回答下列問題：
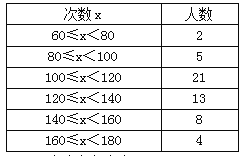
（1）全班有多少人？
（2）組距、組數是多少？
（3）跳繩次數在100≤x＜140范圍內同學有多少人，占全班的百分之幾（精確到0.01%）？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在直角坐標系中，正方形A1B1C1O1、A2B2C2C1、…、AnBnCnCn﹣1按如圖所示的方式放置，其中點A1、A2、A3、…、An均在一次函數y=kx+b的圖象上，點C1、C2、C3、…、Cn均在x軸上．若點B1的坐標為（1，1），點B2的坐標為（3，2），則點An的坐標為 ． 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
