
在平面直角坐標(biāo)系![]() 中,A、B為反比例函數(shù)
中,A、B為反比例函數(shù)![]()
![]() 的圖象上兩點(diǎn),A點(diǎn)的橫坐標(biāo)與B點(diǎn)的縱坐標(biāo)均為1,將
的圖象上兩點(diǎn),A點(diǎn)的橫坐標(biāo)與B點(diǎn)的縱坐標(biāo)均為1,將![]()
![]() 的圖象繞原點(diǎn)O順時(shí)針旋轉(zhuǎn)90°,A點(diǎn)的對(duì)應(yīng)點(diǎn)為
的圖象繞原點(diǎn)O順時(shí)針旋轉(zhuǎn)90°,A點(diǎn)的對(duì)應(yīng)點(diǎn)為![]() ,B點(diǎn)的對(duì)應(yīng)點(diǎn)為
,B點(diǎn)的對(duì)應(yīng)點(diǎn)為![]() .
.
(1)求旋轉(zhuǎn)后的圖象解析式;
(2)求![]() 、
、![]() 點(diǎn)的坐標(biāo);
點(diǎn)的坐標(biāo);
(3)連結(jié)![]() .動(dòng)點(diǎn)
.動(dòng)點(diǎn)![]() 從
從![]() 點(diǎn)出發(fā)沿線段
點(diǎn)出發(fā)沿線段![]() 以每秒1個(gè)單位長(zhǎng)度的速度向終點(diǎn)
以每秒1個(gè)單位長(zhǎng)度的速度向終點(diǎn)![]() 運(yùn)動(dòng);動(dòng)點(diǎn)
運(yùn)動(dòng);動(dòng)點(diǎn)![]() 同時(shí)從
同時(shí)從![]() 點(diǎn)出發(fā)沿線段
點(diǎn)出發(fā)沿線段![]() 以每秒1個(gè)單位長(zhǎng)度的速度向終點(diǎn)
以每秒1個(gè)單位長(zhǎng)度的速度向終點(diǎn)![]() 運(yùn)動(dòng),當(dāng)其中一個(gè)點(diǎn)停止運(yùn)動(dòng)時(shí)另一個(gè)點(diǎn)也隨之停止運(yùn)動(dòng).設(shè)運(yùn)動(dòng)的時(shí)間為
運(yùn)動(dòng),當(dāng)其中一個(gè)點(diǎn)停止運(yùn)動(dòng)時(shí)另一個(gè)點(diǎn)也隨之停止運(yùn)動(dòng).設(shè)運(yùn)動(dòng)的時(shí)間為![]() 秒,試探究:是否存在使
秒,試探究:是否存在使![]() 為等腰直角三角形的
為等腰直角三角形的![]() 值,若存在,求出
值,若存在,求出![]() 的值;若不存在,說(shuō)明理由.
的值;若不存在,說(shuō)明理由.
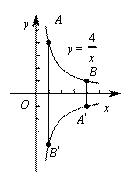
解:(1)如圖所示,∵點(diǎn)![]() 關(guān)于
關(guān)于![]() 軸的對(duì)稱點(diǎn)為
軸的對(duì)稱點(diǎn)為![]() ,
,![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,
,
 ∴
∴![]() ⊥
⊥![]() 軸于
軸于![]() ,
,![]() ,
,
![]() .…………………………1分
.…………………………1分
∴![]() .
.
∴![]() ,
,
由題意可知 ![]() ,
, ![]() .
.
∴![]() .
.
過(guò)點(diǎn)![]() 作
作![]() 軸于
軸于![]() ,
,![]() 軸于
軸于![]() ,
,
在![]() 中,
中,![]() ,
, ![]() .
.
由矩形![]() 得
得![]() .
.
∵點(diǎn)![]() 在第四象限∴
在第四象限∴![]() .……………………………2分
.……………………………2分
(2)設(shè)經(jīng)過(guò)![]() 、
、![]() 、
、![]() 三點(diǎn)的拋物線的解析式為
三點(diǎn)的拋物線的解析式為![]() .
.
依題意得 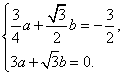 ………………………3分
………………………3分
解得 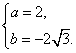 ∴此拋物線的解析式為
∴此拋物線的解析式為![]() .………………………4分
.………………………4分
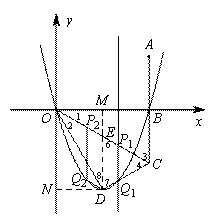
(3)∵![]() ,
,
∴點(diǎn)![]() 為拋物線的頂點(diǎn).
為拋物線的頂點(diǎn).
∴直線![]() 為拋物線的對(duì)稱軸,交
為拋物線的對(duì)稱軸,交![]() 于
于![]() ,
,
由題意可知 ![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等邊三角形,
是等邊三角形,![]() .
.
∴![]() .
.
①當(dāng)點(diǎn)![]() 在
在![]() 上時(shí),四邊形
上時(shí),四邊形![]() 為等腰梯形.
為等腰梯形.
∵![]() ∥
∥![]() ∥
∥![]() ,
,![]() 與
與![]() 不平行,∴四邊形
不平行,∴四邊形![]() 為梯形.
為梯形.
要使梯形![]() 為等腰梯形,只需滿足
為等腰梯形,只需滿足![]() .
.
∵![]() ,∴點(diǎn)
,∴點(diǎn)![]() 在
在![]() 上.
上.
由![]() 、
、![]() 求得直線
求得直線![]() 的解析式為
的解析式為![]() .
.
又∵點(diǎn)![]() 在拋物線上,∴
在拋物線上,∴![]() .
.
解得![]() (與點(diǎn)
(與點(diǎn)![]() 重合,舍).∴
重合,舍).∴![]() 點(diǎn)橫坐標(biāo)為
點(diǎn)橫坐標(biāo)為![]() .
.
由![]() 、
、![]() 求得直線
求得直線![]() 的解析式為
的解析式為![]() .
.
∵點(diǎn)![]() 在
在![]() 上,∴
上,∴![]() .∴
.∴![]() .………6分
.………6分
②當(dāng)點(diǎn)![]() 在
在![]() 上時(shí),四邊形
上時(shí),四邊形![]() 為平行四邊形,此時(shí)
為平行四邊形,此時(shí)![]() 點(diǎn)坐標(biāo)為
點(diǎn)坐標(biāo)為![]() . ……………………8分
. ……………………8分
綜上所述,當(dāng)![]() 時(shí),
時(shí),![]() 為等腰梯形;當(dāng)
為等腰梯形;當(dāng)![]() 時(shí),
時(shí),![]() 為平行四邊形.
為平行四邊形.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
 坐標(biāo)原點(diǎn).A、B兩點(diǎn)的橫坐標(biāo)分別是方程x2-4x-12=0的兩根,且cos∠DAB=
坐標(biāo)原點(diǎn).A、B兩點(diǎn)的橫坐標(biāo)分別是方程x2-4x-12=0的兩根,且cos∠DAB=
| ||
| 2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
 18、在平面直角坐標(biāo)系中,把一個(gè)圖形先繞著原點(diǎn)順時(shí)針旋轉(zhuǎn)的角度為θ,再以原點(diǎn)為位似中心,相似比為k得到一個(gè)新的圖形,我們把這個(gè)過(guò)程記為【θ,k】變換.例如,把圖中的△ABC先繞著原點(diǎn)O順時(shí)針旋轉(zhuǎn)的角度為90°,再以原點(diǎn)為位似中心,相似比為2得到一個(gè)新的圖形△A1B1C1,可以把這個(gè)過(guò)程記為【90°,2】變換.
18、在平面直角坐標(biāo)系中,把一個(gè)圖形先繞著原點(diǎn)順時(shí)針旋轉(zhuǎn)的角度為θ,再以原點(diǎn)為位似中心,相似比為k得到一個(gè)新的圖形,我們把這個(gè)過(guò)程記為【θ,k】變換.例如,把圖中的△ABC先繞著原點(diǎn)O順時(shí)針旋轉(zhuǎn)的角度為90°,再以原點(diǎn)為位似中心,相似比為2得到一個(gè)新的圖形△A1B1C1,可以把這個(gè)過(guò)程記為【90°,2】變換.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com