
【題目】![]() 中,
中,![]() ,
,![]() ,
,![]() 的半徑長是
的半徑長是![]() ,當
,當![]() 時,
時,![]() 與直線
與直線![]() 的位置關系是________;當
的位置關系是________;當![]() 時,
時,![]() 與直線
與直線![]() 的位置關系是________.
的位置關系是________.
【答案】相交 相切
【解析】
據題意畫出相應的圖形,然后過C作CD與AB垂直,垂足為D,在直角三角形ACD中,由30°角所對的直角邊等于斜邊的一半,由斜邊AB的長和面積定值求出CD的長,即為圓心到直線的距離,小于圓C的半徑,可得圓C與直線AB相交;當∠A=45°時,求出CD的長和圓的半徑2比較大小即可.
根據題意畫出圖形,如圖所示:
當∠A=30°,
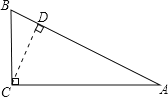
過C作CD⊥AB,交AB于點D,
在Rt△ACD中,∵AB=4,∠A=30°,
∴BC=![]() AB=2,
AB=2,
∴AC=![]() =2
=2![]() ,
,
∴CD=![]() AC=
AC=![]() ,
,
又∵圓C的半徑為2,則![]() <2,
<2,
∴CD<R,
∴則⊙C與AB的位置關系是相交,
故答案為:相交;
當∠A=45°時,
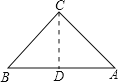
過C作CD⊥AB,交AB于點D,
在Rt△ACD中,∵AB=4,∠A=45°,
∴AB=AC,
∴CD=![]() AB=2,
AB=2,
又∵圓C的半徑為2,則CD=R,
∴則⊙C與AB的位置關系是相切.
故答案為:相切.


科目:初中數學 來源: 題型:
【題目】某農場學校積極開展陽光體育活動,組織了九年級學生定點投籃,規定每人投籃3次.現對九年級(1)班每名學生投中的次數進行統計,繪制成如下的兩幅統計圖,根據圖中提供的信息,回答下列問題.
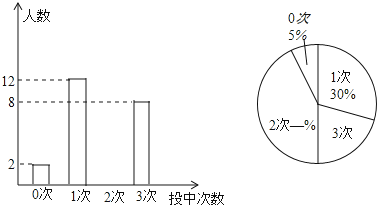
(1)求出九年級(1)班學生人數;
(2)補全兩個統計圖;
(3)求出扇形統計圖中3次的圓心角的度數;
(4)若九年級有學生200人,估計投中次數在2次以上(包括2次)的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
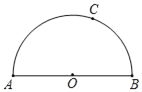
【題目】如圖,AB為半圓O的直徑,點C為半圓上任一點.
(1)若∠BAC=30°,過點C作半圓O的切線交直線AB于點P.求證:△PBC≌△AOC;
(2)若AB=6,過點C作AB的平行線交半圓O于點D.當以點A,O,C,D為頂點的四邊形為菱形時,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB>AC,∠BAC的平分線交外接圓于D,DE⊥AB于E,DM⊥AC于M.
(1)求證:BE=CM.
(2)求證:AB﹣AC=2BE.
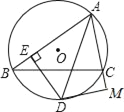
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】張康和李健兩名運動愛好者周末相約到丹江環庫綠道進行跑步鍛煉.
(1)周日早上![]() 點,張康和李健同時從家出發,分別騎自行車和步行到離家距離分別為
點,張康和李健同時從家出發,分別騎自行車和步行到離家距離分別為![]() 千米和
千米和![]() 千米的綠道環庫路入口匯合,結果同時到達,且張康每分鐘比李健每分鐘多行
千米的綠道環庫路入口匯合,結果同時到達,且張康每分鐘比李健每分鐘多行![]() 米,求張康和李健的速度分別是多少米
米,求張康和李健的速度分別是多少米![]() 分?
分?
(2)兩人到達綠道后約定先跑![]() 千米再休息,李健的跑步速度是張康跑步速度的
千米再休息,李健的跑步速度是張康跑步速度的![]() 倍,兩人在同起點,同時出發,結果李健先到目的地
倍,兩人在同起點,同時出發,結果李健先到目的地![]() 分鐘.
分鐘.
①當![]() ,
,![]() 時,求李健跑了多少分鐘?
時,求李健跑了多少分鐘?
②求張康的跑步速度多少米![]() 分?(直接用含
分?(直接用含![]() ,
,![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠B=45°,∠ACB=60°,AB=16,AD⊥BC,垂足為D,∠ACB的平分線交AD于點E,則AE的長為( )
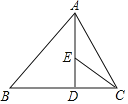
A.![]() B.4
B.4![]() C.
C.![]()
![]() D.6
D.6![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形 ABCD 中,AB=4,AD=3,M 是邊 CD 上一點,將△
ADM 沿直線 AM 對折,得到△AMM.
(1)當 AN 平分∠MAB 時,求 DM 的長;
(2)連接 BN,當 DM=1 時,求 BN 的長.
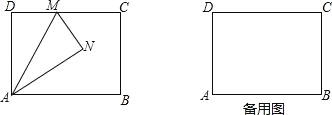
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法中,正確說法的個數有( )
①角是軸對稱圖形,對稱軸是角的平分線;②等腰三角形至少有![]() 條對稱軸,至多有
條對稱軸,至多有![]() 條對稱軸;③關于某直線對稱的兩個三角形一定是全等三角形;④兩圖形關于某直線對稱,對稱點一定在直線的兩旁.
條對稱軸;③關于某直線對稱的兩個三角形一定是全等三角形;④兩圖形關于某直線對稱,對稱點一定在直線的兩旁.
A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com