
【題目】小賢與小杰在探究某類二次函數問題時,經歷了如下過程:
求解體驗
(1)已知拋物線![]() 經過點(-1,0),則
經過點(-1,0),則![]() = ,頂點坐標為 ,該拋物線關于點(0,1)成中心對稱的拋物線的表達式是 .
= ,頂點坐標為 ,該拋物線關于點(0,1)成中心對稱的拋物線的表達式是 .
抽象感悟
我們定義:對于拋物線![]() ,以
,以![]() 軸上的點
軸上的點![]() 為中心,作該拋物線關于
為中心,作該拋物線關于
點![]() 對稱的拋物線
對稱的拋物線![]() ,則我們又稱拋物線
,則我們又稱拋物線![]() 為拋物線
為拋物線![]() 的“衍生拋物線”,點
的“衍生拋物線”,點![]() 為“衍生中心”.
為“衍生中心”.
(2)已知拋物線![]() 關于點
關于點![]() 的衍生拋物線為
的衍生拋物線為![]() ,若這兩條拋物線有交點,求
,若這兩條拋物線有交點,求![]() 的取值范圍.
的取值范圍.
問題解決
(3) 已知拋物線![]()
①若拋物線![]() 的衍生拋物線為
的衍生拋物線為![]() ,兩拋物線有兩個交點,且恰好是它們的頂點,求
,兩拋物線有兩個交點,且恰好是它們的頂點,求![]() 的值及衍生中心的坐標;
的值及衍生中心的坐標;
②若拋物線![]() 關于點
關于點![]() 的衍生拋物線為
的衍生拋物線為![]() ,其頂點為
,其頂點為![]() ;關于點
;關于點![]() 的衍生拋物線為
的衍生拋物線為![]() ,其頂點為
,其頂點為![]() ;…;關于點
;…;關于點![]() 的衍生拋物線為
的衍生拋物線為![]() ,其頂點為
,其頂點為![]() ;…(
;…(![]() 為
為
正整數).求![]() 的長(用含
的長(用含![]() 的式子表示).
的式子表示).

【答案】求解體驗: ![]() ;頂點坐標是(-2,1);
;頂點坐標是(-2,1);![]() ;抽象感悟:
;抽象感悟:![]() ;問題解決:①
;問題解決:①![]() ;(0,6);②
;(0,6);②![]()
【解析】(1)把(-1,0)代入![]() 即可未出
即可未出![]() =-4,然后把拋物線解析式變為頂點式即可求得拋物線的頂點坐標,繼而可得頂點關于(0,1)的對稱點,從而可寫出原拋物線關于點(0,1)成中心對稱的拋物線的表達式;
=-4,然后把拋物線解析式變為頂點式即可求得拋物線的頂點坐標,繼而可得頂點關于(0,1)的對稱點,從而可寫出原拋物線關于點(0,1)成中心對稱的拋物線的表達式;
(2)先求出拋物線 ![]() 的頂點是(-1,6),從而求出 (-1,6)關于
的頂點是(-1,6),從而求出 (-1,6)關于![]() 的對稱點是
的對稱點是![]() ,得
,得 ![]() ,根據兩拋物線有交點,可以確定方程
,根據兩拋物線有交點,可以確定方程 ![]() 有解,繼而求得m的取值范圍即可;
有解,繼而求得m的取值范圍即可;
(3) ①先求出拋物線![]() 以及拋物線
以及拋物線![]() 的衍生拋物線為
的衍生拋物線為![]() ,的頂點坐標,根據兩拋物線有兩個交點,且恰好是它們的頂點,求
,的頂點坐標,根據兩拋物線有兩個交點,且恰好是它們的頂點,求![]() 的值及再根據中點坐標公式即可求出衍生中心的坐標;
的值及再根據中點坐標公式即可求出衍生中心的坐標;
② 如圖,設![]() ,
,![]() …
… ![]() ,
,![]() 與
與![]() 軸分別相于
軸分別相于![]() ,
,![]() …
… ![]() ,
,![]() ,則
,則![]() ,
,![]() ,…
,… ![]() ,
,![]() 分別關于
分別關于![]() ,
,![]() …
…![]() ,
,![]() 中心對稱,由題意則可得
中心對稱,由題意則可得![]() ,
,![]() …
… ![]() 分別是△
分別是△![]() ,
,![]() …
…![]() 的中位線,繼而可得
的中位線,繼而可得![]() ,
,![]() ,…
,… ![]() ,再根據點的坐標即可求得
,再根據點的坐標即可求得![]() 的長.
的長.
求解體驗
(1)把(-1,0)代入![]() 得
得![]() ,
,
∴![]() ,
,
∴頂點坐標是(-2,1),
∵(-2,1)關于(0,1)的對稱點是(2,1),
∴成中心對稱的拋物線表達式是:![]() ,
,
即 ![]() (如圖)
(如圖)

抽象感悟
(2) ∵ ![]() ,
,
∴ 頂點是(-1,6),
∵ (-1,6)關于![]() 的對稱點是
的對稱點是![]() ,
,
∴ ![]() ,
,
∵ 兩拋物線有交點,
∴ ![]() 有解,
有解,
∴ ![]() 有解,
有解,
∴ ![]() ,
,
∴ ![]() ;(如圖)
;(如圖)
問題解決
(3) ① ∵![]() =
=![]() ,
,
∴ 頂點(-1,![]() ),
),
代入 ![]() 得:
得:![]() ①
①
∵ ![]() ,
,
∴ 頂點(1,![]() ),
),
代入 ![]() 得:
得:![]() ②
②
由① ② 得 ![]() ,
,
∵ ![]() ,
,![]() ,
,
∴ ![]() ,
,
∴ 兩頂點坐標分別是(-1,0),(1,12),
由中點坐標公式得“衍生中心”的坐標是(0,6);
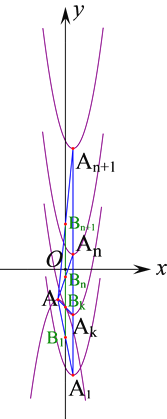
② 如圖,設![]() ,
,![]() …
… ![]() ,
,![]() 與
與![]() 軸分別相于
軸分別相于![]() ,
,![]() …
… ![]() ,
,![]() ,
,
則![]() ,
,![]() ,…
,… ![]() ,
,![]() 分別關于
分別關于![]() ,
,![]() …
…![]() ,
,![]() 中心對稱,
中心對稱,
∴![]() ,
,![]() …
… ![]() 分別是△
分別是△![]() ,
,![]() …
…![]() 的中位線,
的中位線,
∴![]() ,
,![]() ,…
,… ![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]()
![]() ]
]![]() .
.


科目:初中數學 來源: 題型:
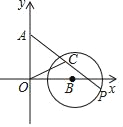
【題目】如圖,在平面直角坐標系中,A(0,3)、B(3,0),以點B為圓心、2為半徑的⊙B上有一動點P.連接AP,若點C為AP的中點,連接OC,則OC的最小值為( )
A. 1 B. ![]() ﹣1 C.
﹣1 C. ![]() D. 2
D. 2![]() ﹣1
﹣1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,拋物線C1:y=ax2﹣2ax+c(a<0)與x軸交于A、B兩點,與y軸交于點C.已知點A的坐標為(﹣1,0),點O為坐標原點,OC=3OA,拋物線C1的頂點為G.
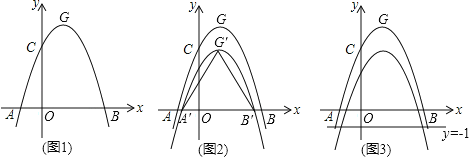
(1)求出拋物線C1的解析式,并寫出點G的坐標;
(2)如圖2,將拋物線C1向下平移k(k>0)個單位,得到拋物線C2,設C2與x軸的交點為A′、B′,頂點為G′,當△A′B′G′是等邊三角形時,求k的值:
(3)在(2)的條件下,如圖3,設點M為x軸正半軸上一動點,過點M作x軸的垂線分別交拋物線C1、C2于P、Q兩點,試探究在直線y=﹣1上是否存在點N,使得以P、Q、N為頂點的三角形與△AOQ全等,若存在,直接寫出點M,N的坐標:若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,我們定義直線![]() 為拋物線
為拋物線![]() 、b、c為常數,
、b、c為常數,![]() 的“夢想直線”;有一個頂點在拋物線上,另有一個頂點在y軸上的三角形為其“夢想三角形”.
的“夢想直線”;有一個頂點在拋物線上,另有一個頂點在y軸上的三角形為其“夢想三角形”.

已知拋物線![]() 與其“夢想直線”交于A、B兩點
與其“夢想直線”交于A、B兩點![]() 點A在點B的左側
點A在點B的左側![]() ,與x軸負半軸交于點C.
,與x軸負半軸交于點C.
![]() 填空:該拋物線的“夢想直線”的解析式為______,點A的坐標為______,點B的坐標為______;
填空:該拋物線的“夢想直線”的解析式為______,點A的坐標為______,點B的坐標為______;
![]() 如圖,點M為線段CB上一動點,將
如圖,點M為線段CB上一動點,將![]() 以AM所在直線為對稱軸翻折,點C的對稱點為N,若
以AM所在直線為對稱軸翻折,點C的對稱點為N,若![]() 為該拋物線的“夢想三角形”,求點N的坐標;
為該拋物線的“夢想三角形”,求點N的坐標;
![]() 當點E在拋物線的對稱軸上運動時,在該拋物線的“夢想直線”上,是否存在點F,使得以點A、C、E、F為頂點的四邊形為平行四邊形?若存在,請直接寫出點E、F的坐標;若不存在,請說明理由.
當點E在拋物線的對稱軸上運動時,在該拋物線的“夢想直線”上,是否存在點F,使得以點A、C、E、F為頂點的四邊形為平行四邊形?若存在,請直接寫出點E、F的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
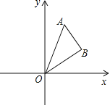
【題目】如圖,在平面直角坐標系![]() 中,點
中,點![]() ,點
,點![]() ,將
,將![]() 繞著點
繞著點![]() 旋轉
旋轉![]() 后得到
后得到![]() .
.
![]() 在圖中畫出
在圖中畫出![]() ;
;
![]() 點
點![]() ,點
,點![]() 的對應點
的對應點![]() ’和
’和![]() ’的坐標分別是
’的坐標分別是![]() ’________和
’________和![]() ’________;
’________;
![]() 請直接寫出
請直接寫出![]() 和
和![]() ’
’![]() ’的數量關系和位置關系.
’的數量關系和位置關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
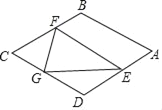
【題目】如圖,在菱形ABCD中,AB=![]() ,∠B=120°,點E是AD邊上的一個動點(不與A,D重合),EF∥AB交BC于點F,點G在CD上,DG=DE.若△EFG是等腰三角形,則DE的長為_____.
,∠B=120°,點E是AD邊上的一個動點(不與A,D重合),EF∥AB交BC于點F,點G在CD上,DG=DE.若△EFG是等腰三角形,則DE的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
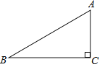
【題目】如圖,已知![]() 的斜邊
的斜邊![]() ,
,![]() .
.
![]() 以點
以點![]() 為圓心作圓,當半徑為多長時,直線
為圓心作圓,當半徑為多長時,直線![]() 與
與![]() 相切?為什么?
相切?為什么?
![]() 以點
以點![]() 為圓心,分別以
為圓心,分別以![]() 和
和![]() 為半徑作兩個圓,這兩個圓與直線
為半徑作兩個圓,這兩個圓與直線![]() 分別有怎樣的位置關系?
分別有怎樣的位置關系?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com