
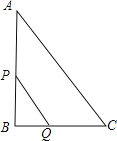
【題目】如圖,Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,現有兩個動點P、Q分別從點A和點B同時出發,其中點P以2cm/s的速度,沿AB向終點B移動;點Q以1cm/s的速度沿BC向終點C移動,其中一點到終點,另一點也隨之停止.連接PQ.設動點運動時間為x秒.
(1)用含x的代數式表示BQ、PB的長度;
(2)當x為何值時,△PBQ為等腰三角形;
(3)是否存在x的值,使得四邊形APQC的面積等于20cm2?若存在,請求出此時x的值;若不存在,請說明理由.
【答案】(1)BQ=x,PB=8﹣2x;(2)![]() ;(3)存在,x=2.
;(3)存在,x=2.
【解析】
(1)根據路程=速度×時間求出BQ,AP,再根據PB=AB-AP即可.
(2)根據題意,當△PBQ為等腰三角形時,BQ=PB,建立一個關于x的方程,解方程即可.
(3)用含x的代數式表示出四邊形APQC的面積,利用四邊形APQC的面積為20建立一個關于x方程,解方程即可.若有解,則存在,若無解則不存在.
解:(1)∵∠B=90°,AC=10,BC=6,
∴AB=8.
∴BQ=x,PB=AB-AP=8﹣2x;
(2)由題意,得
8﹣2x=x,
∴x=![]() .
.
∴當x=![]() 時,△PBQ為等腰三角形;
時,△PBQ為等腰三角形;
(3)假設存在x的值,使得四邊形APQC的面積等于20cm2,
則![]()
解得x1=x2=2.
假設成立,所以當x=2時,四邊形APQC面積的面積等于20cm2.


科目:初中數學 來源: 題型:
【題目】學校準備在校園內修建一個矩形的綠化帶,矩形的面積為定值,它的一邊長![]() 與另一邊長
與另一邊長![]() 之間的函數圖像如圖.
之間的函數圖像如圖.

(1)該綠化帶的面積是多少?寫出![]() 與
與![]() 的函數解析式.
的函數解析式.
(2)完成下表,并回答問題:如果該綠化帶的長![]() 不得超過
不得超過![]() ,那么
,那么![]() 應控制在什么范圍?
應控制在什么范圍?
| 10 | 20 | 30 | 40 |
|
查看答案和解析>>
科目:初中數學 來源: 題型:
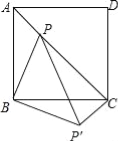
【題目】如圖,P為正方形ABCD內一點,且BP=2,PC=3,∠APB=135°,將△APB繞點B順時針旋轉90°得到△CP′B,連接PP′,則AP= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,直線CD與以線段OB為直徑的半⊙A相切于點C,連接OC、BC,作OD⊥CD,垂足為D,OB=10,
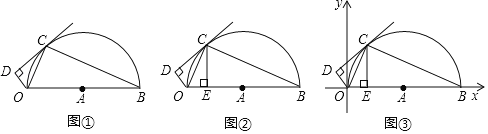
(1)求證:∠OCD=∠OBC;
(2)如圖②,作CE⊥OB于點E,若CE=AE,求線段OD的長;
(3)如圖③,在(2)的條件下,以O點為原點建立平面直角坐標系求△DOB外接圓的圓心坐標.
以下是優優和樂樂兩位同學對第(3)小題的討論
優優:這題很簡單嘛,我只要求出這個三角形任意兩條邊的中垂線解析式,然后求交點坐標就行了.樂樂:我還有其他的好方法.
如果你是樂樂,你會怎么做?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 與
與![]() 都是等腰直角三角形,且
都是等腰直角三角形,且![]() ,
,![]() ,連接DC,點M、P、N分別為DE、DC、BC的中點
,連接DC,點M、P、N分別為DE、DC、BC的中點
(1)如圖1,當點D、E分別在邊AB、AC上,線段PM與PN的數量關系是______,位置關系是______;
(2)把等腰![]() 繞點A旋轉到如圖2的位置,連接MN,判斷
繞點A旋轉到如圖2的位置,連接MN,判斷![]() 的形狀,并說明理由;
的形狀,并說明理由;
(3)把等腰![]() 繞點A在平面內任意旋轉,
繞點A在平面內任意旋轉,![]() ,
,![]() ,請直接寫出
,請直接寫出![]() 的面積S的變化范圍.
的面積S的變化范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
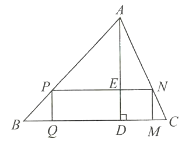
【題目】如圖所示,![]() 是一塊銳角三角形余料,邊
是一塊銳角三角形余料,邊![]() 毫米,高
毫米,高![]() 毫米,要把它加工成一個矩形零件,使矩形的一邊在
毫米,要把它加工成一個矩形零件,使矩形的一邊在![]() 上,其余兩個頂點分別在
上,其余兩個頂點分別在![]() ,
,![]() 上,設該矩形的長
上,設該矩形的長![]() 毫米,寬
毫米,寬![]() 毫米.
毫米.
(1)求證:![]() ;
;
(2)當![]() 與
與![]() 分別取什么值時,矩形
分別取什么值時,矩形![]() 的面積最大?最大面積是多少?
的面積最大?最大面積是多少?
(3)當矩形![]() 的面積最大時,它的長和寬是關于
的面積最大時,它的長和寬是關于![]() 的一元二次方程
的一元二次方程![]() 的兩個根,而
的兩個根,而![]() ,
,![]() 的值又恰好分別是
的值又恰好分別是![]() ,10,12,13,
,10,12,13,![]() 這5個數據的眾數與平均數,試求
這5個數據的眾數與平均數,試求![]() 與
與![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
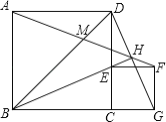
【題目】如圖,![]() 、
、![]() 是正方形,
是正方形,![]() 在
在![]() 上,直線
上,直線![]() 、
、![]() 交于
交于![]() ,且
,且![]() ,
,![]() 、
、![]() 交于
交于![]() ,當
,當![]() 在線段
在線段![]() (不與
(不與![]() 、
、![]() 重合)上運動時,下列四個結論:①
重合)上運動時,下列四個結論:①![]() ;②
;②![]() 、
、![]() 所夾的銳角為
所夾的銳角為![]() ;③
;③![]() ;④若
;④若![]() 平分
平分![]() ,則正方形
,則正方形![]() 的面積為4,其中結論正確的是__(填序號)
的面積為4,其中結論正確的是__(填序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
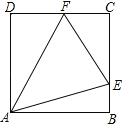
【題目】如圖正方形ABCD,E、F分別為BC、CD邊上一點.
(1)若∠EAF=45°,求證:EF=BE+DF;
(2)若該正方形ABCD的邊長為1,如果△CEF的周長為2.求∠EAF的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
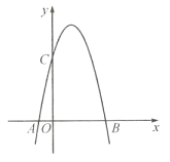
【題目】如圖,一個二次函數的圖像經過![]() 、
、![]() 、
、![]() 三點,點
三點,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 在
在![]() 軸的正半軸上,且
軸的正半軸上,且![]() .
.
(1)求點![]() 的坐標;
的坐標;
(2)求這個二次函數的解析式;
(3)自變量![]() 在什么范圍內時,
在什么范圍內時,![]() 隨
隨![]() 的增大而增大?何時,
的增大而增大?何時,![]() 隨
隨![]() 的增大而減小
的增大而減小
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com