
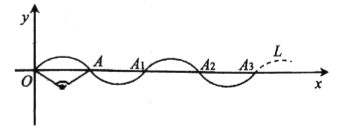
【題目】曲線![]() 在直角坐標系中的位置如圖所示,曲線
在直角坐標系中的位置如圖所示,曲線![]() 是由半徑為2,圓心角為
是由半徑為2,圓心角為![]() 的
的![]() (
(![]() 是坐標原點,點
是坐標原點,點![]() 在
在![]() 軸上)繞點
軸上)繞點![]() 旋轉
旋轉![]() ,得到
,得到![]() ;再將
;再將![]() 繞點
繞點![]() 旋轉
旋轉![]() ,得到
,得到![]() ;……依次類推,形成曲線
;……依次類推,形成曲線![]() ,現有一點
,現有一點![]() 從
從![]() 點出發,以每秒
點出發,以每秒![]() 個單位長度的速度,沿曲線
個單位長度的速度,沿曲線![]() 向右運動,則點
向右運動,則點![]() 的坐標為___________;在第
的坐標為___________;在第![]() 時,點
時,點![]() 的坐標為____________.
的坐標為____________.
科目:初中數學 來源: 題型:
【題目】如圖,一次函數![]() 的圖象分別交x軸、y軸于C,D兩點,交反比例函數
的圖象分別交x軸、y軸于C,D兩點,交反比例函數![]() 圖象于A(
圖象于A(![]() ,4),B(3,m)兩點.
,4),B(3,m)兩點.
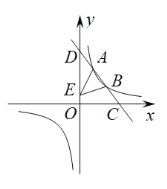
(1)求直線CD的表達式;
(2)點E是線段OD上一點,若![]() ,求E點的坐標;
,求E點的坐標;
(3)請你根據圖象直接寫出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場計劃購進![]() 、
、![]() 兩種新型節能臺燈共
兩種新型節能臺燈共![]() 盞,這兩種臺燈的進價、售價如表所示:
盞,這兩種臺燈的進價、售價如表所示:

(![]() )若商場預計進貨款為
)若商場預計進貨款為![]() 元,則這兩種臺燈各購進多少盞?
元,則這兩種臺燈各購進多少盞?
(![]() )若商場規定
)若商場規定![]() 型臺燈的進貨數量不超過
型臺燈的進貨數量不超過![]() 型臺燈數量的
型臺燈數量的![]() 倍,應怎樣進貨才能使商場在銷售完這批臺燈時獲利最多?此時利潤為多少元?
倍,應怎樣進貨才能使商場在銷售完這批臺燈時獲利最多?此時利潤為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,對角線互相垂直的四邊形叫做垂美四邊形.
(1)概念理解:如圖2,在四邊形![]() 中,
中,![]() ,問四邊形
,問四邊形![]() 是垂美四邊形嗎?請說明理由;
是垂美四邊形嗎?請說明理由;
(2)性質探究:如圖1,四邊形![]() 的對角線
的對角線![]() 交于點
交于點![]() ,
,![]() .
.
試證明:![]() ;
;
(3)解決問題:如圖3,分別以![]() 的直角邊
的直角邊![]() 和斜邊
和斜邊![]() 為邊向外作正方形
為邊向外作正方形![]() 和正方形
和正方形![]() ,連結
,連結![]() .已知
.已知![]() ,求
,求![]() 的長.
的長.
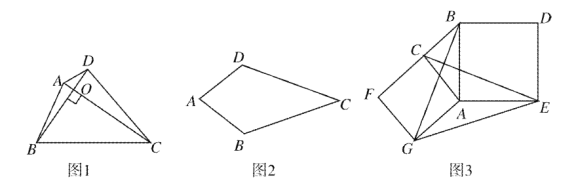
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著生活節奏的加快以及智能手機的普及,外賣點餐逐漸成為越來越多用戶的餐飲消費習慣.由此催生了一批外賣點餐平臺,已知某外賣平臺的送餐費用與送餐距離有關(該平臺只給5千米范圍內配送),為調査送餐員的送餐收入,現從該平臺隨機抽取80名點外賣的用戶進行統計,按送餐距離分類統計結果如下表:
送餐距離x(千米) | 0 | 1 | 2 | 3 | 4 |
數量 | 12 | 20 | 24 | 16 | 8 |
(1)從這80名點外賣的用戶中任取一名用戶,該用戶的送餐距離不超過3千米的概率為 ;
(2)以這80名用戶送餐距離為樣本,同一組數據取該小組數據的中間值(例如第二小組(1<x ≤2)的中間值是1.5),試估計利用該平臺點外賣用戶的平均送餐距離;
(3)若該外賣平臺給送餐員的送餐費用與送餐距離有關,不超過2千米時,每份3元;超過2千米但不超4千米時,每份5元;超過4千米時,每份9元. 以給這80名用戶所需送餐費用的平均數為依據,若送餐員一天的目標收入不低于150元,試估計一天至少要送多少份外賣?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,點O在射線![]() 上(點
上(點![]() 不與點
不與點![]() 重合),過點
重合),過點![]() 作
作![]() ,垂足為
,垂足為![]() ,以點
,以點![]() 為圓心,
為圓心,![]() 為半徑畫半圓
為半徑畫半圓![]() ,分別交射線
,分別交射線![]() 于
于![]() 、
、![]() 兩點,設
兩點,設![]() .
.
(1)如圖,當點![]() 為
為![]() 邊的中點時,求
邊的中點時,求![]() 的值;
的值;
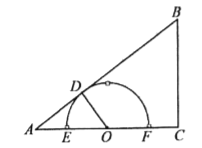
(2)如圖,當點![]() 與點
與點![]() 重合時,連接
重合時,連接![]() ,求弦
,求弦![]() 的長;
的長;
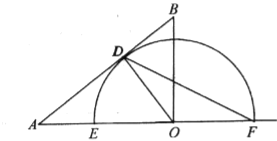
(3)當半圓![]() 與
與![]() 無交點時,直接寫出
無交點時,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題情境:
在綜合與實踐課上,老師讓同學們以“矩形紙片的剪拼”為主題開展數學活動.如圖1,將矩形紙片![]() 沿對角線
沿對角線![]() 剪開,得到
剪開,得到![]() 和
和![]() .并且量得
.并且量得![]() ,
,![]() .
.
操作發現:
(1)將圖1中的![]() 以點
以點![]() 為旋轉中心,按逆時針方向旋轉
為旋轉中心,按逆時針方向旋轉![]() ,使
,使![]() ,得到如圖2所示的
,得到如圖2所示的![]() ,過點
,過點![]() 作
作![]() 的平行線,與
的平行線,與![]() 的延長線交于點
的延長線交于點![]() ,則四邊形
,則四邊形![]() 的形狀是________.
的形狀是________.
(2)創新小組將圖1中的![]() 以點
以點![]() 為旋轉中心,按逆時針方向旋轉,使
為旋轉中心,按逆時針方向旋轉,使![]() 、
、![]() 、
、![]() 三點在同一條直線上,得到如圖3所示的
三點在同一條直線上,得到如圖3所示的![]() ,連接
,連接![]() ,取
,取![]() 的中點
的中點![]() ,連接
,連接![]() 并延長至點
并延長至點![]() ,使
,使![]() ,連接
,連接![]() 、
、![]() ,得到四邊形
,得到四邊形![]() ,發現它是正方形,請你證明這個結論.
,發現它是正方形,請你證明這個結論.
實踐探究:
(3)縝密小組在創新小組發現結論的基礎上,進行如下操作:將![]() 沿著
沿著![]() 方向平移,使點
方向平移,使點![]() 與點
與點![]() 重合,此時
重合,此時![]() 點平移至
點平移至![]() 點,
點,![]() 與
與![]() 相交于點
相交于點![]() ,如圖4所示,連接
,如圖4所示,連接![]() ,試求
,試求![]() 的值.
的值.
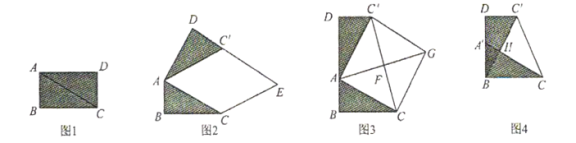
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】陳先生駕車從杭州到上海,要經過一段高速公路,假設汽車在高速公路上勻速行駛,記行駛時間為t小時,速度為v千米/小時,如果陳先生駕車速度為90千米/小時,2小時可以通過高速公路.
(1)求v與t的函數表達式.
(2)高速公路的速度限定為不超過120千米/小時,陳先生計劃10:00駛入高速,11:48前駕駛離開高速公路,求它的駕車速度v的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
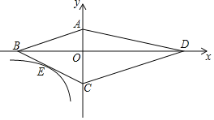
【題目】如圖,四邊形ABCD的頂點都在坐標軸上,若AB∥CD,![]() AOB與
AOB與![]() COD面積分別為8和18,若雙曲線y=
COD面積分別為8和18,若雙曲線y=![]() 恰好經過BC的中點E,則k的值為_____.
恰好經過BC的中點E,則k的值為_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com