
【題目】如圖所示,四邊形ABCD的對(duì)角線(xiàn)AC , BC相交于點(diǎn)O , 下列判斷正確的是( ) 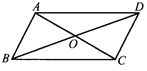
A.若AO=OC , 則ABCD是平行四邊形,
B.若AC=BD , 則ABCD是平行四邊形,
C.若AO=BO , CO=DO , 則ABCD是平行四邊形,
D.若AO=OC , BO=OD , 則ABCD是平行四邊形.
【答案】D
【解析】A只是一條對(duì)角線(xiàn)平分,不正確,B是對(duì)角線(xiàn)相等,沒(méi)有此定理,不正確,C對(duì)角線(xiàn)不一定平分,只有D是對(duì)角線(xiàn)互相平分,故選D.
【考點(diǎn)精析】解答此題的關(guān)鍵在于理解平行四邊形的判定的相關(guān)知識(shí),掌握兩組對(duì)邊分別平行的四邊形是平行四邊形:兩組對(duì)邊分別相等的四邊形是平行四邊形;一組對(duì)邊平行且相等的四邊形是平行四邊形;兩組對(duì)角分別相等的四邊形是平行四邊形;對(duì)角線(xiàn)互相平分的四邊形是平行四邊形.


 名師導(dǎo)航單元期末沖刺100分系列答案
名師導(dǎo)航單元期末沖刺100分系列答案 名校名卷單元同步訓(xùn)練測(cè)試題系列答案
名校名卷單元同步訓(xùn)練測(cè)試題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】給出下列說(shuō)法:①一條直線(xiàn)的平行線(xiàn)只有一條;②過(guò)一點(diǎn)與已知直線(xiàn)平行的直線(xiàn)只有一條;③平行于同一條直線(xiàn)的兩條直線(xiàn)平行;④經(jīng)過(guò)直線(xiàn)外一 點(diǎn),有且只有一條直線(xiàn)與這條直線(xiàn)平行.其中正確的有( )
A. 1個(gè) B. 2個(gè) C. 3個(gè) D. 4個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知點(diǎn)A(﹣1,﹣2),B關(guān)于拋物線(xiàn)y=a(x﹣1)2的對(duì)稱(chēng)軸對(duì)稱(chēng),則點(diǎn)B的坐標(biāo)為( )
A.(1,﹣2)
B.(﹣1,2)
C.(2,﹣2)
D.(3,﹣2)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列結(jié)論:①點(diǎn)(3,2)與(2,3)是同一個(gè)點(diǎn);②點(diǎn)(0,-2)在x軸上;③點(diǎn)(0,0)是坐標(biāo)原點(diǎn);④點(diǎn)(1,1)在第二象限;⑤點(diǎn)(2,0)在x軸的正半軸上.其中正確的是____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】用配方法把二次函數(shù)y=x2+4x﹣5化成y=a(x﹣h)2+k的形式并寫(xiě)出頂點(diǎn)坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知關(guān)于x的方程x2﹣4x+m=0有兩個(gè)不相等的實(shí)數(shù)根,那么m的取值范圍是_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】將拋物線(xiàn)y=x2+2向上平移1個(gè)單位后所得新拋物線(xiàn)的表達(dá)式為_____.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com